2020.05.04.26
Files > Volume 5 > Vol 5 No 4 2020
Modeling the strategies to eradicate rats introduced in the Galapagos Islands
Camila Velastegui1, Mary Pulgar-Sánchez2, *, Kevin Chamorro3
http://dx.doi.org/10.21931/RB/2020.05.04.26
ABSTRACT
The Galapagos Islands are well known for their incredible biodiversity and the inspiration for Charles Darwin's natural evolution theory. It is an ecosystem that has evolved without predators, so their native species are unfit for competition. As a result, this biodiversity has been threatened by invasive species like rats (Black and Norwegian). Nowadays, the primary strategy to control rats is by having drones that disperse a unique poisoned bait. Our study aims to mathematically model the strategies to eradicate rats in islands, based on previously reported processes. As a result, we are obtaining the approximated time to reduce its population as much as being eradicated, without threatening the coexisting species. We also propose a suitable alternative to be applied in the Galapagos Islands to recover their biodiversity richness. We find that rats' introduction has caused a decrease in the native species due to having specific traits that make them fitter in different situations. The best method to control species in such a sensitive environment is by the use of anticoagulant rodenticides. The current method used for eradicating rats seems to be the most profitable even though there is not enough information to see the collateral consequences of the poison technique. Furthermore, we propose this theoretical study complemented with in situ samplings to corroborate our hypothesis and improve our prediction model.
Keywords: invasive species, rodenticides, eradication, prediction model, strategies, Galapagos Islands
INTRODUCTION
Islands developed as isolated ecosystems resulted in species evolution with restricted native competence and the inability to compete with predators. Then the presence of foreign species directly treats island biodiversity worldwide. The introduction of mammals, specifically the presence of invasive rodents, is among the most problematic species in islands1 by being responsible for changes in the ecosystem and many extinctions to date2. There are records of invasive rodents on 80% of the significant islands globally, and how it is still unceasingly introduced3 that worries conservationists. Rodents represent more than a problem for the conservation of biodiversity; they are a threat to humans' health with whom overlap its habitat by being an imminent disease vector4. The rats' ease of adaptation, lifespan, and rapid spread, complemented by the warm, favorable climate of the islands, have made rats a tricky pest to deal with5.
The need to recover species and restore island conservation has driven the development of eradication techniques as one of the most cost-effective tools6, even though in large islands, this is often impossible7. Eradication of invasive species is based on (i) all target animals (rodents) are put at risk by the eradication technique(s), (ii) target animals must be removed at a rate exceeding their rate of increase at all densities, (iii) immigration must be zero8. However, native species are also at risk. So, this requires special attention. Meanwhile, the process must be done as fast as possible to avoid eliminating a new generation of invaders. Eradication is performed by delivering a lethal dose of rodenticide to each rodent; this bait containing rodenticide can be distributed either by hand-broadcast or in bait stations on small islands, but for larger islands, eradication by an aerial broadcast of bait is required to ensure suitable bait availability5,9,10. However, there is a failure rate of 16.1% of eradication from the overall eradication processes reported5,11. Mathematical models and, in particular, models applied to biology can be an essential tool to understand the dynamics of a phenomenon12, which allows the prediction of the impact of a determined process with variables pre-established that saves monetary, ecological investment, labor, and time.
Galapagos Islands are an exact representation of biodiversity; however, it has been affected by introducing the rodents Rattus rattus, R. norvegicus, R. exulans, and Mus musculus13 that arrive at the archipelago on whaling boats and pirate ships since the late 1600s14. Human colonies spread together with rats' dispersing along the island at unknown dates of arrival15. These introduced species caused a decrease in the population of endemic species principally in two ways: the first one is eating the eggs and the second by eating the other species' food. The Galapagos Islands have always been a key example of Charles Darwin's theory of evolution. Though, the species he detected at the time has been gradually lost. Darwin recorded in 1835, the first species of the black rat on the island Santiago and progressively new researchers recorded more rodent species16. Black rats drove the extinction of four endemic rodents and a terminal decline of fauna, to mention sea- and land-bird populations and even the endangered status of one race of giant tortoise16–18. At present, there are two endemic genera of rats, Oryzomys and Nesoryzomys16.
In Galapagos Islands, there have been attempts to eradicate rodents; one of them occurred in 1988 at Pinzon Island with rodenticide bait dumps and hand broadcast of baits containing brodifacoum and coumatetralyl that were unsuccessful19,20. North Seymour Island was hand baited in 2007 with wax blocks containing brodifacoum and successfully eradicating black rats21. The first aerial broadcast of brodifacoum baits occurred in 2011 at Rabida and Pinzon Islands and managed to eliminate invasive black rats. For this procedure, it captured and held the Pinzon tortoises (Chelonoidis ephippium), Pinzon lava lizards (Microlophus duncanensis), and Galapagos hawks (Buteo galapagoensis) species to mitigate the direct impact of the rodenticide15,22. The rodenticide bait has led to non-target animals' poisoning, especially raptors whose diet is not restricted only to rodents23. For instance, in 2011, after the eradication plan in Pinzon, all captive Galapagos hawks were released, and from days to months later, it was found that 22 of them died by anticoagulant toxicosis by brodifacoum in the liver due to rodenticide exposition of lava lizards, part of hawks diet13,24.
This paper aims to evaluate an alternative use of rodenticide with reduced secondary effects and obtain a theoretical approximation by designing a mathematical equation that may predict the process before being applied in situ. Simultaneously, suggesting the control and management of strategies to eradicate rats in the Galapagos Islands. All based on the successful plans carried out in other case studies to promote the conservation of endemic species in the archipelago and avoid the rapid extinction of more species. Our study begins with an analysis of the three main strategies for eradicating rats, where the assumptions for our study are introduced. The base equation for our mathematical model is then shown and is followed by the model equations along with each parameter and estimated value to use. Then, in results and discussion, the best alternatives and the eradication time of rats in the Galapagos Islands are analyzed and compared. Finally, this work ends with the conclusions of our study and future work.
METHODS
Eradication strategies and model assumptions
We had considered three main strategies for the eradication of rats. The first strategy is poisoning, the second is killing by trapping, and the third one is inducing infertility.
The poisoning strategy is based on the use of rodenticides that had been broadly applied in rat eradication programs, some with success and others with some failures6. Anticoagulant rodenticides are the most widely used poisoned technique. They inhibit the synthesis of clotting factors dependent on vitamin-K in the liver, which results in internal hemorrhaging, leading to death typically within 3–10 days25. The rodenticides are designed specially to kill rats, although non-target species could also be affected. There are some reports about the affection of non-target species due to rodenticides, especially in vertebrates66. The rate of success of rodenticide use depends on rats' ability to differentiate the toxins, which produce offspring capable of avoiding bait stations. For our model, we assume that the poisoning strategy is by using bait stations and that eventually, the rats will learn how to distinguish poison.
The second method analyzed is the use of traps, which are more acceptable within urban populations27. Trapping is recommended for sensitive environments where rat populations are prominent, as it has the most significant capture rate. The use of traps needs continuous monitoring, which requires more costs, but at the same time, it avoids affecting the capture of non-target species and also can be used as a way of monitoring the rat population within an island. This is an essential parameter before assisting the application of any eradication methods28. The use of traps also induces the development of trap shyness such that they learn to avoid traps. For that reason, a period of pre-baiting to familiarize the rats with the traps is recommended29. Due to this, the strategy could have a small-time lag from their initiation of the trap strategy and population decrease. Therefore, the use of traps is more recommended in places with high human density. In the Galapagos Islands, it is recommended in the populated islands, which are Baltra (Seymour), Floreana, Santa Cruz, San Cristóbal, and Isabela, and with a large population of rats. In our model, we assume that live traps are widely distributed in the islands and that rats will learn to avoid traps.
The third strategy consists of inducing sterility. The use of chemosterilants could have changed the behavior and structure of the population. Induced sterilty may be temporary or permanent and can affect males or females30. Depending on how the sterility is induced by chemosterilants or modified females' introduction, different outcomes could arise. In the Galapagos Islands, where it is not recommended to introduce any new animal, it is suggestable to induce infertility by chemosterilants like androgens. The sterilization strategy has higher specificity than traps. One of the main disadvantages of sterilization is the time lag between sterilization and decreased population size. In the present study, we applied the sterile induced in females because female rats mate several times (higher than 90 per hour with different males)30. The sterilization method that we are considering is the spread of androgens that induce infertility in females. We are assuming that rats do not learn how to identify the androgen bait. Just one intervention with androgen is needed, and we induce sterility for the remaining of the rat's lifetime.
In addition to the eradication methods described above, we also consider joining two strategies to get a better output of rats' eradication in the islands. For this purpose, we consider the case of applying poisoning and sterilization strategy. The assumptions will be the same as the eradication methods. The other assumptions for this method are applied at the same time. So, the same rate of rats dying from poison could be infertile or fertile.
Application of the Logistic equation
Rat populations grow in an essentially logistic pattern until the limit of the habitat's carrying capacity is approached30. It means that rat populations tend to increase exponentially, but they lower their increasing rate when the carrying capacity is reached. We had constructed our equations modeling the different eradication methods based on the logistic equation [1], where r is the rate of population increase. N is the number of individuals in the population. K is the carrying capacity31. We are assuming no time lags, no migration among islands or with the continent, and no influence of genetic variation.

To evaluate the best method to control rats, we varied the parameter "r" that regulates the increased population rate. For each method, we are calculating "r" that will result from the strategy applied. We consider that each eradication method has a different r. The calculation of r depends on the rate of births and deaths to the population. All the calculations and rates presented were defined by months.
Four factors will influence the rate of births. The first factor is the proportion of adults in the population (γ). In the model presented, we consider as an adult the population capable of producing offspring. The second factor is the average offspring that a rat produces per month (α). The third parameter is the female proportion within the population because they are the ones that produce offspring, so they are the ones that produce an increase in the population (β). For this parameter, the value of 0.5 is assumed, which means equal proportions. This is due to various reports showing there was an equal distribution of gender within the rats. The last factor is the fertility rate of females (δ), which is directly correlated with the proportion of pregnant female rats.
The rate of deaths is the sum of the rate of rats that die naturally (ω) and rats that die due to the eradication method. In our case, just the first method of eradication, the use of poison, we consider the rate of natural deaths and rats' rate died by poison. This last rate is calculated, considering that rats learn how to distinguish the poison. The equation developed by Gentry in 1971 describes this rate [2], where ϕ is the rate of rats dying by poison A1, is the fraction of rats that will be poisoned if the rats will not realize that they are being poisoned, Q is the fraction of rats that do not learn to distinguish poison, and A2 describes how fast the rats learn how to distinguish poison32.
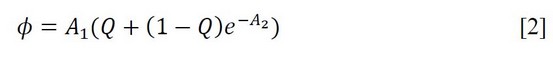
The second method of eradication is very similar to the first method because here, we also had rats that learn to avoid traps. Therefore, the rate of rats dying by traps will be influenced by B1 (the fraction of rats that will be trapped if the rats will not realize that they are being trapped). P is the fraction of rats that do not learn to distinguish traps and B2 describes how fast the rats learn how to distinguish traps32.
For the third eradication method, the deaths will be just influenced by the fraction of rats that die due to natural causes. The change in this equation is the fertility rate that will decrease due to the induced sterility (i). . In the mixed strategies, we are using the same parameters as their respective eradication methods.
Model Equations and parameters of the Strategies analyzed
Summarizing all the descriptions above, we developed the following equations for the eradication methods. Equations [3], [4], [5], [6] describes the poisoning strategy, trapping strategy, sterilization strategy, and the combination of poisoning and infertility strategies, respectively:
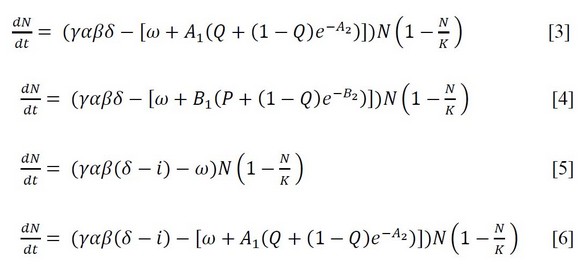
The values of the parameters described before were estimated from previous reports about the behavior of rats. In some cases, the parameters calculated were an average of various reports. The values and parameters are summarized in Table 1.
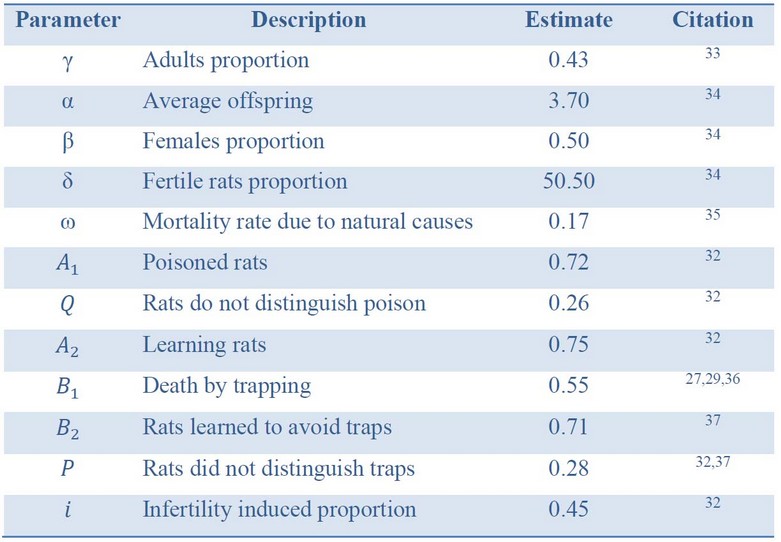
Table 1. Values of the parameters used in the calculations
After finding all the parameters, we calculate the respective "r" values and then replace them in the logistic equation solution [7]. For the estimation of the carrying capacity, we calculated based on the total area of the islands that had rats in Galapagos, which is 6937 km2 22, and the home range of rats being 150 square feet 38. To estimate the rats' initial population on the island, we consider the density of 4.6 rats per ha reported on one island of Galapagos 39.

RESULTS AND DISCUSSION
To find the best strategy to eradicate rats, we must first solve each of the differential equations presented in [3],[4], and [5]. The results obtained considering the previous variables and restrictions presented by the model are presented in Fig. 1. We discover that the strategy that produces a more significant reduction is by poison with -0.20, the second is induced infertility with -0.12, and the trapping method with -0.11. It can be seen that the strategy of spreading poison is the one that makes our logistic equation tend to 0 more quickly.
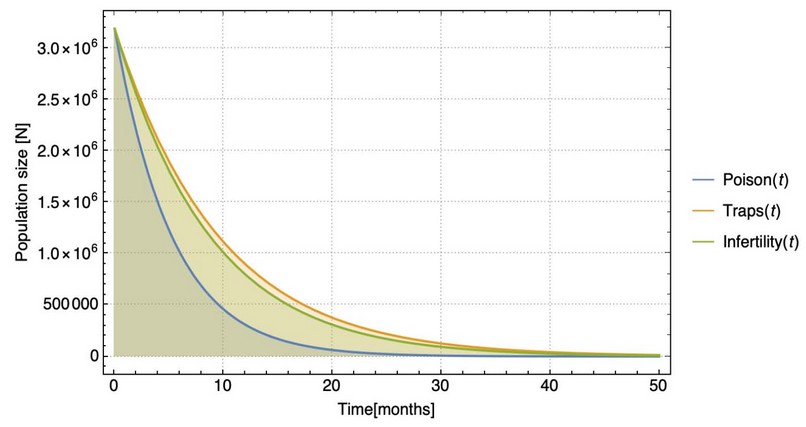
Figure 1. Population growth of the application of the three strategies.
The primary data found for the poison methodology to be most significant is the value of the intrinsic growth rate, which will influence rats' data that learn about the detection of the poison or the trap it is pretending to use. Besides, this data is highly influenced if we contrast it with the logistic equation's solution [4] since they are strictly within an exponential. So it will be what predominates for the behavior at zero that is expected for eradication. On the other hand, the infertility strategy has a supervised factor since the population of infertile rats must be better controlled with the rat eradication process. If we contrast it with equation [3], we observe that the variable induced infertility ratio is the independent variable with more weight to give a better growth rate. The poison propagation strategy is one of the most common to be used according to the reviewed literature, which suggests that it is the most effective strategy in the different places that have been applied.
Figure 2. Map of the Islands that have registered the presence of rats
As we can see in Fig. 1, even though poisoning is the best strategy, it does not result in the ideal time to reduce rats' population because if there is a long enough time lag, there could be a resurgence of rats. There have been reports that approximately after 2 years, there is a relapse of rat infestations and the percentage of rat incidence increase along the time40. However, when we used two techniques, it had a better result in eradicating rats, as shown in Fig. 3. The mixed strategy of poisoning and sterility the ones with highest values we got an r of -0.52 and got an eradication before two years, which ultimately is the aim.
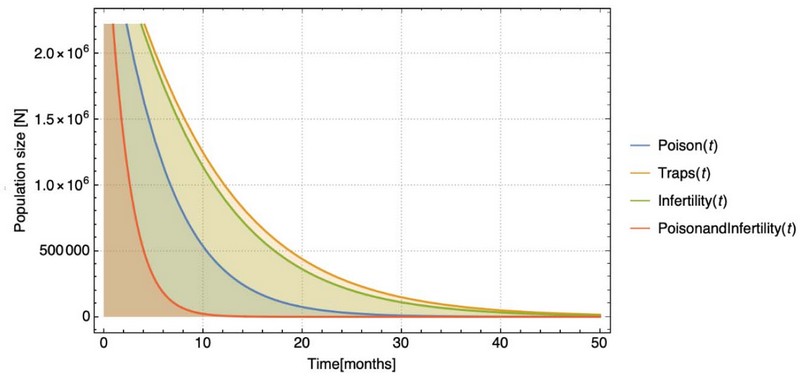
Figure 3. Population growth of the 3 strategies and the combination of poison and infertility
With the results obtained, it is possible to consider the predicted times for the eradication of rats in each of the islands belonging to the Galapagos Archipelago that have the presence of rats as in Fig. 2, representing a population of rats N = 1 for each one of them and time in months. Therefore, in the solution of the logistic regression equation [6], we will be able to obtain the different times (t) according to the area in square kilometers (km2) in which rats are exterminated applying the poison strategy. The results are presented in Table 2.
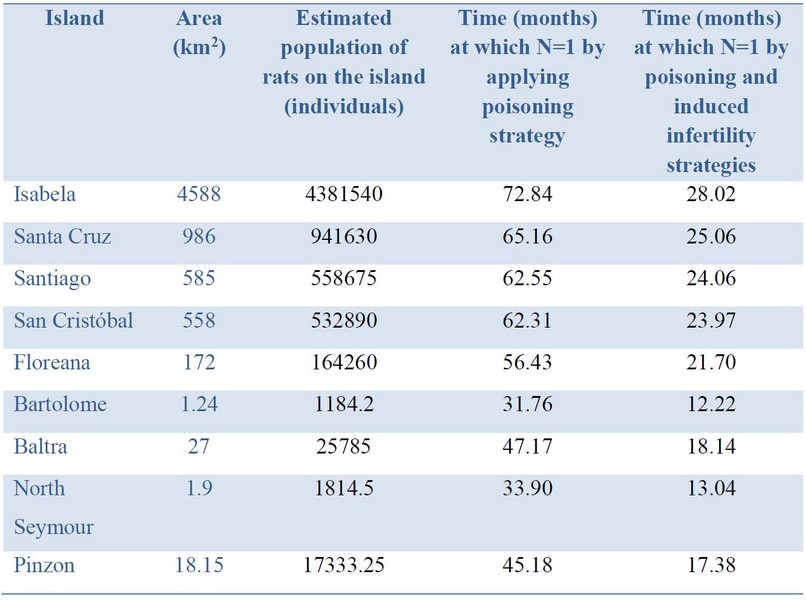
Table 2. Area of each island with the presence of rats registered and the predicted time to reach population equals 1
As we can see, the larger the island area, the longer it will take to eradicate rats, having a direct relationship between the area of the island and time. Still, the time of poisoning with rodenticide, despite being found as the most effective, takes a prolonged time, but this time is reduced notably if complemented with the other strategies. This fact is essential when avoiding new births since the generation time of rats is short.
CONCLUSIONS
The best strategy to recover biodiversity after the ecosystem has been affected by alien species' introduction is its eradication. The most viable and effective way found is the use of rodenticides and their dispersion through bait stations. The most widely used rodenticide is an anticoagulant of second-generation brodifacoum. The eradication time is dependent on the area of the island and its rodent population density. By combining the poisoning and sterility induced strategies, time is significantly reduced compared to the individual application. In the case of the Galapagos archipelago, Isabela Island needs the most time with 28.02 months, while the island we can eliminate rodents the fastest is Bartolomé, the smallest, in about a year. It has to be taken into account that the target animals inhabit the island, but if it is human-populated and if there are animals that coexist in the same habitat.
The application of a mathematical model to this situation allows us to simulate the eradication of rats without the need to experiment in situ, which is the best in the least amount of time. This allows us to save financial expenses and time to carry out this work. It is crucial to have actual data from the islands to improve the model and get closer to real-time to offer better suggestions regarding invasive species' eradication processes.
Future work
We look forward to finding a budget for the studio and monitoring the ecology of rodents in the Galapagos Islands and how it has affected biodiversity. There is insufficient quantitative information on the critical archipelago and introduced species of rodents. With this, we will continue to improve our mathematical model and subsequently form part of a rescue plan for the site's critical biodiversity.
REFERENCES
1 Hilton GM, Cuthbert RJ. The catastrophic impact of invasive mammalian predators on birds of the UK Overseas Territories: A review and synthesis. Ibis (Lond 1859) 2010; 152: 443–458.
2 Towns DR, Atkinson IAE, Daugherty CH. Have the harmful effects of introduced rats on islands been exaggerated? Biol Invasions 2006; 8: 863–891.
3 Atkinson I, Western D, Pearl MC. Introduced animals and extinctions. In: Conservation for the twenty-first century. Oxford University Press: New York, 1989, pp 54–79.
4 Fundación Charles Darwin (FCD) y WWF-Ecuador. Atlas de Galápagos, Ecuador: Especies Nativas e Invasoras. 2018.
5 Russell JC, Holmes ND. Tropical island conservation: Rat eradication for species recovery. Biol Conserv 2015; 185: 1–7.
6 Howald G, Donlan CJ, Galván JP, Russell JC, Parkes J, Samaniego A et al. Invasive rodent eradication on islands. Conserv Biol 2007; 21: 1258–1268.
7 Duron Q, Shiels AB, Vidal E. Control of invasive rats on islands and priorities for future action. Conserv Biol 2017; 31: 761–771.
8 Cromarty P, Broome K, Cox A, Empson RA, Hutchinson WM, McFadden I. Eradication planning for invasive alien species on islands – the approach developed by the New Zealand department of conservation. Turn Tide Erad Invasive Species 2002; : 85–91.
9 Pott M, Wegmann AS, Griffiths R, Samaniego-Herrera A, Cuthbert RJ, Brooke M de L et al. Improving the odds: Assessing bait availability before rodent eradications to aid in selecting bait application rates. Biol Conserv 2015; 185: 27–35.
10 Pitt WC, Driscoll LC, Sugihara RT. Efficacy of rodenticide baits for the control of three invasive rodent species in Hawaii. Arch Environ Contam Toxicol 2011; 60: 533–542.
11 Brown D, Tershy B, Pitt WC, Cuthbert RJ, Wegmann A, Keitt B et al. Successes and failures of rat eradications on tropical islands : a comparative review of eight recent projects. 2019; : 120–130.
12 Delgadillo Alemán ES, Carrillo Kú AR, Vela Arévalo LV. Modelación matemática del control de plagas en un cultivo de brócoli. Rev del Dpto Matemáticas y Física la UAA 2006; : 3–20.
13 Rueda D, Carrion V, Castano P, Cunninghame F, Fisher P, Hagen E et al. Preventing extinctions: planning and undertaking invasive rodent eradication from Pinzon Island, Galapagos. invasives scaling up to meet challenge Occas Pap SSC 2019; : 51–56.
14 Patton JL, Yang SY, Myers P. Genetic and morphologic divergence among introduced rat populations (rattus rattus) of the galÁpagos archipelago, ecuador. Syst Biol 1975; 24: 296–310.
15 Patton JL, Hafner MS. Biosystematics of the Native Rodents of the Galapagos Archipielago, Ecuador. Patterns Evol Galapagos Org 1983; : 539–567.
16 Key G, Muñoz EH. Distribution and current status of rodents in the Galápagos. Not Galapagos 1994; 53: 21–25.
17 Cruz JB, Cruz F. Conservation of the Dark-rumped Petrel Pterodroma phaeopygia of the Galápagos Islands, 1982-1991. Bird Conserv Int 1996; 6: 23–32.
18 Steadman DW, Stafford TW, Donahue DJ, Jull AJT. Chronology of Holocene vertebrate extinction in the Galápagos Islands. Quat Res 1991; 36: 126–133.
19 Harper GA, Zabala J, Carrion V. Monitoring of a population of Galápagos land iguanas (Conolophus subcristatus) during a rat eradication using brodifacoum. Isl invasives Erad Manag 2011; : 309–312.
20 Cayot L, Rassmann K, Tillmich F. Are marine iguanas endangered on islands with introduced predators. Not … 1994; : 3–5.
21 Harper G., Carrion V. Introduced rodent in the Galapagos: colonisation, removal and the future. Isl Invasives Erad Manag Proc Int Conf Isl Invasives 2011; : 63–66.
22 Campbell KJ, Carrión V, Sevilla C. Increasing the scale of successful invasive rodent eradications in the Galapagos Islands. Galapagos Rep 2011-2012 2013; : 194–198.
23 Nakayama SMM, Morita A, Ikenaka Y, Mizukawa H, Ishizuka M. A review: Poisoning by anticoagulant rodenticides in non-target animals globally. J Vet Med Sci 2019; 81: 298–313.
24 Rueda D, Campbell KJ, Fisher P, Cunninghame F, Ponder JB. Biologically significant residual persistence of brodifacoum in reptiles following invasive rodent eradication, Galapagos Islands, Ecuador. Conserv Evid 2016; 13: 38.
25 Hadler MR, Sahdbolt. RS. Novel 4-hydroxycoumarin anticoagulants active against resistant rats. Nature 1975; 253: 277–282.
26 Booth L, Eason C, Spurr E. Literature review of the acute toxicity and persistence of brodifacoum to invertebrates. Sci Conserv 2001; : 1–9.
27 Roomaney R, Ehrlich R, Rother H-A. The acceptability of rat trap use over pesticides for rodent control in two poor urban communities in South Africa. Environ Health 2012; 11: 32.
28 Ji W, Craig J. An evaluation of the efficiency of rodent trapping methods: The effect of trap arrangement, cover type, and bait. N Z J Ecol 1999; 23.
29 Thompson H V. Experimental live trapping of rats, with observations on their behaviour. Br J Anim Behav 1953; 1: 96–111.
30 Jackson WB. Biological and behavioural studies of rodents as a basis for control. Bull World Health Organ 1972; 47: 281–286.
31 Gotelli N. Gotelli_2008_A primer of Ecology (4ed).pdf. 2008.
32 Gentry JW. Evaluation of Rat Eradication Programs. Environ Sci Technol 1971; 5: 704–709.
33 Morlan HB, Bernice C. U, Dent JE. DOMESTIC rats, rat ectoparasites and typhus control. Public Health Monogr 1952; 14: 1–37.
34 Panti-May JA, Carvalho-Pereira TSA, Serrano S, Pedra GG, Taylor J, Pertile AC et al. A Two-Year Ecological Study of Norway Rats (Rattus norvegicus) in a Brazilian Urban Slum. PLoS One 2016; 11: e0152511–e0152511.
35 Davis DE. The Characteristics of Rat Populations. Q Rev Biol 1953; 28: 373–401.
36 Theuerkauf J, Rouys S, Jourdan H. Efficiency of a New Reverse-Bait Trigger Snap Trap for Invasive Rats and a New Standardised Abundance Index. Ann Zool Fennici 2011; 48: 308–318.
37 Taylor KD, Hammond LE, Quy RJ. The Reactions of Common Rats to Four Types of Live-Capture Trap. J Appl Ecol 1974; 11: 453–459.
38 Brown RZ. Biological Factors in Domestic Rodent Control: Training Guide. U.S. Consumer Protection and Environmental Health Service, Environmental Control Administration, 1969https://books.google.com.ec/books?id=h0o9Gu_CSFQC.
39 Harper GA, Bunbury N. Invasive rats on tropical islands: Their population biology and impacts on native species. Glob Ecol Conserv 2015; 3: 607–627.
40 Smith WW. Rat, Flea, and Murine Typhus Recurrence Following Eradication Measures. Public Health Rep 1958; 73: 469–474.
Received: 10 July 2020
Accepted:10 November 2020
Camila Velastegui1, Mary Pulgar-Sánchez2, *, Kevin Chamorro3
1 School of Biological Sciences and Engineering, Yachay Tech University, Hacienda San José s/n, San Miguel de Urcuquí. (ORCID: https://orcid.org/0000-0002-0340-6247)
2 School of Biological Sciences and Engineering, Yachay Tech University, Hacienda San José s/n, San Miguel de Urcuquí. (ORCID: https://orcid.org/0000-0001-5966-9065) *corresponding author: [email protected]
3 School of Mathematical and Computational Sciences, Yachay Tech University, Hacienda San José s/n, San Miguel de Urcuquí. (ORCID https://orcid.org/0000-0002-7725-3538)
