2021.06.02.23
Files > Volume 6 > Vol 6 No 4 2021 > Vol 6 No 2 2021
INVESTIGATION / RESEARCH
Predicción temporal del número de muertes por lesiones causadas por tránsito en Estados Unidos
Temporal prediction of the number of deaths from traffic accidents in the United States
Javier Rodríguez-Velásquez1*, María Alejandra González-Bernal2, Adiela Ruiz-Gómez3, Esmeralda Guzmán-de la Rosa4, Daniel Pallejá-Lopez5, Freddy Barrios-Arroyave6, Oscar Valero-Alvarado7, Ribká Soracipa-Muñoz8, Nathalia López-Sardoth9, Jorge Rodríguez-Hernandez10
Available from: http://dx.doi.org/10.21931/RB/2021.06.02.23
RESUMEN
Los estudios realizados hasta el momento sobre el comportamiento de los accidentes de tráfico han sido descriptivos; sin embargo, este comportamiento al ser estudiado como un sistema dinámico cuya evolución es predecible en el tiempo ha llevado al diseño de una nueva metodología matemática la cual establece órdenes a una aparente imprevisibilidad, el objetivo del presente estudio es predecir mediante la dinámica probabilística de caminata aleatoria y probabilidad. de la tasa de mortalidad por accidentes de tránsito en los Estados Unidos al 2013. El comportamiento de la tasa de mortalidad por accidentes de tránsito en los Estados Unidos se analiza para el período 1994-2012 desde un contexto físico y matemático, estableciendo longitudes de análisis probabilístico y probabilístico de cuatro espacios, para determinar relativo un aumento anual consecutivo y disminuciones que es la tasa de fatalidades probable tránsito 2013. En el 2013 Estados Unidos informó que la tasa de mortalidad por accidentes de tránsito fue de 10,35 por 100.000 habitantes, el valor previsto fue de 10,6, logrando una tasa de éxito del 98% del valor real. El comportamiento dinámico de las víctimas mortales de tráfico en Estados Unidos, según un orden matemático de causalidad en el que fue posible predecir la tasa de víctimas mortales de tránsito para 2013.
Palabras clave: mortalidad, accidentes de tránsito, trauma, lesiones.
ABSTRACT
Studies so far to the behaviour of traffic accidents have been descriptive; however, this behaviour to be studied as a dynamic system whose evolution is predictable over time has led to the design of new mathematical methodology which establishes orders to an apparent unpredictability, the objective of the present study is to predict by probabilistic random walk dynamics and probability of death rate from traffic accidents in the United States by 2013. The behaviour of the death rate from traffic accidents in the United States is analysed for the period between 1994-2012 from a physical and mathematical context, by setting lengths probabilistic and probabilistic analysis of four spaces, to determine relative a consecutive annual increase and decreases which is the rate of fatalities likely 2013 transit. 2013 United States reported that the death rate from traffic accidents was 10.35 per 100,000 inhabitants, the predicted value was 10.6, achieving a success rate of 98% of the actual value. The dynamic behaviour of traffic fatalities in the United States, according to a mathematical acausal order in which it was possible to predict the rate of traffic fatalities by 2013.
Keywords: mortality, traffic accidents, trauma, injuries.
INTRODUCCIÓN
De acuerdo a la teoría de la probabilidad, en un experimento, la totalidad de posibles resultados se denomina espacio muestral; la probabilidad es un concepto que permite calcular que tan posible es un resultado respecto al espacio muestral.1,2 Para el cálculo de la probabilidad de sucesos equiprobables se utiliza generalmente la Regla de Laplace3, el cálculo de la probabilidad se basa en su definición axiomática4 que establece que la probabilidad presenta valores entre 0 y 1, la probabilidad del espacio muestral es igual a 1 y la probabilidad de ocurrencia dos o más eventos independientes es igual al producto de sus probabilidades individuales. La probabilidad permite estudiar fenómenos que son variables pero que son en promedio consistentes.2
Otro de los conceptos aplicados a fenómenos con un comportamiento irregular y que está asociado con la probabilidad, es la caminata al azar, término acuñado por Karl Pearson en 1905,5 este término puede entenderse en su forma más simple si imaginamos un caminante en un sistema coordenado, que inicia su movimiento en el origen,6 desplazándose aleatoriamente hacia valores positivos o negativos dando un paso de longitud también aleatoria, por lo algunas veces retrocederá y otras avanzará; lo que podríamos decir acerca del movimiento del caminante es cuál es el cuadrado de su desplazamiento medio, el cual está en función del número (N) de pasos dados.2 Con la caminata al azar se puede acotar un movimiento probabilista, encontrando rangos de valores numéricos que permitan establecer predicciones, este concepto ha sido aplicado a diversos campos como la ecología, biología, economía entre otros.7-13
De acuerdo al reporte mundial de seguridad vial de la WHO14 las lesiones de tránsito han sido declarados como un problema de salud pública. De acuerdo a estimaciones hechas por la misma entidad, a nivel mundial más de 1,2 millones de personas fallecen por esta causa y alrededor de 50 millones quedan afectadas,14 se destaca que las tasas de mortalidad por inseguridad vial por 100.000 habitantes son recurrentemente inversamente proporcionales a los ingresos de los países.15 Este fenómeno se ha asociado a diferentes factores de riesgo: beber y conducir, el exceso de velocidad y el no uso de cascos en las motocicletas, no portar cinturones de seguridad y sistemas de retención infantil, sumándose recientemente a estos el uso de dispositivos móviles.16
Como consecuencia al gran número de información que se debe manejar en estudios de tipo, descriptivo, geográfico, demográfico y de revisión documental para el análisis de las variables se hace uso de metodologías estadísticas de corte prospectivo y retrospectivo.17,18 En un estudio retrospectivo realizado para el análisis de muertes relacionadas con el vehículo todo terreno (ATV), durante el periodo comprendido entre los años 1985-2006,19 consideraron para el estudio todo análisis de información descriptiva y multivariada, encontrando que la disminución del uso de este tipo de vehículos en carretera podría ser una manera eficaz de reducir las muertes.
Por otro lado, estudios realizados para medir el impacto que tiene las lesiones causadas por el tránsito (LCT)18 y su asociación con mortalidad, han evaluado la posible contribución de los sistemas organizados de atención de trauma, en la disminución de la mortalidad por accidentes causadas por el tránsito.20 Han concluido que la disminución muertes causadas por el tránsito, se debe a la contribución de los protocolos de atención aplicados en traumatología, sin dejar de lado los planes de prevención realizados por otras instituciones.
Otro tipo de epidemias como el dengue y la malaria han sido estudiadas a partir de metodologías desarrolladas en el contexto de la física y la matemática, logrando evaluar la complejidad de su comportamiento como sistemas dinámicos predecibles,21-25 estableciendo ordenes matemáticos a causales, que permiten la predicción de la epidemia. A partir de la probabilidad y la entropía se desarrollaron predicciones de brotes de malaria en 810 municipios de Colombia, encontrando un porcentaje de precisión del 99,86%. También, a partir de una analogía con la caminata al azar probabilista, se desarrolló un método predictivo de la dinámica de dengue en Colombia, estableciendo predicciones superiores al 90%,22 de igual forma esta metodología se ha utilizado también para establecer predicciones y proyecciones del comportamiento de la obesidad infantil en Estados Unidos.25
El presente estudio tiene como propósito predecir el número de muerte causadas por lesiones tránsito en Estados Unidos para el año 2013, mediante la caminata al azar probabilista,22 valor que será posteriormente comparado con el reportado para este año por el NHTSA (National Highway Traffic Safety Administration).]
METODOS
Longitud de la tasa de muertes por lesiones causadas por tránsito: representa el valor de la tasa de muertes por lesiones causadas por tránsito la cual se calcula mediante la siguiente ecuación:22

Siendo,y las coordenadas para el año inicial y son las coordenadas para el año siguiente.
Longitud probabilista de la tasa de muertes por lesiones causadas por tránsito: es el primer espacio de probabilidad que considera cada variación anual de la longitud L de muertes por lesiones causadas por tránsito como un evento mediante la siguiente ecuación:

Probabilidad de la tasa de muertes por lesiones causadas por tránsito: se calcula en el segundo espacio de probabilidad y es el cociente entre la tasa de muertes por accidente de tránsito y la suma total de la tasa de muertes reportadas durante el periodo comprendido entre los años 1994-2012 mediante la siguiente ecuación:

Desviación media cuadrática: Para evaluar si en el segundo espacio de probabilidad existen probabilidades cargadas de la tasa de muertes por accidente de tránsito se usa la siguiente fórmula:

Siendo N la suma total de las tasas de muertes por accidente de tránsito registradas durante el periodo comprendido entre los años 1994-2013 en Estados Unidos, que en términos probabilistas lo que se está analizando es la totalidad de eventos del espacio muestral.
Ecuación de segundo grado para la predicción de muertes por lesiones causadas por tránsito: Para la predicción se tomó los valores de las longitudes hallada con la ecuación 1 de los tres años anteriores al año 2013, construyendo de esta manera un tercer espacio de probabilidad. Luego fue remplazado el promedio aritmético de la probabilidad hallado para estos tres últimos años y el valor de la suma de las tres longitudes (TL) en la siguiente ecuación:

Para determinar cuál de los dos valores de la predicción hallados para el 2013 con la ecuación 5 es el evento más probable en relación a de si hay una disminución (D) o aumento (A) de la tasa de muertes por accidente de tránsito respecto al año 2012, se construyó un cuarto espacio de probabilidad para estudiar el comportamiento de períodos consecutivos de dos y tres años.
Procedimiento
Se tomaron los valores anuales de la tasa de muertes de tránsito en Estados Unidos del periodo comprendido entre los años 1994-2012 de la base de datos de NHTSA.2
Se evaluó la dinámica del comportamiento de la tasa de muertes por accidente de tránsito en Estados Unidos graficando estos valores en un plano cartesiano, ubicando en el eje x los años y en el eje y la tasa de muertes por accidente de tránsito, para luego analizar su comportamiento en analogía a una caminata al azar probabilista (ver figura 1).
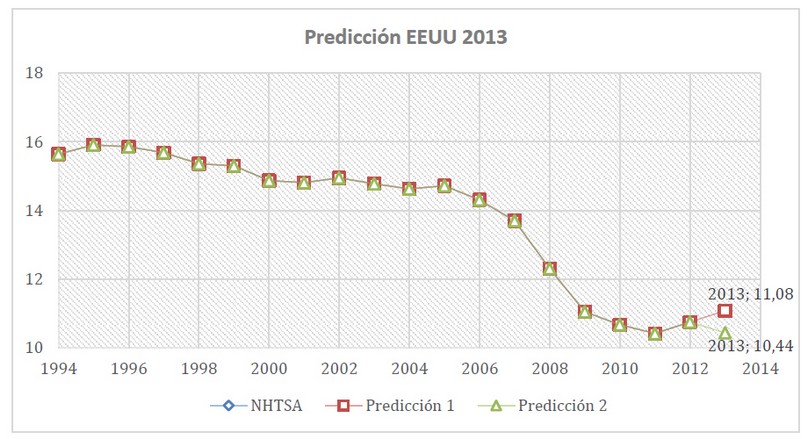
Figure 1. Superposición de los dos valores predichos para la tasa de muertes por accidente de tránsito en Estados Unidos para el año 2013. Trazado continuo corresponde al valor 11,08, y el trazado discontinuo, corresponde al valor 10,44. Todos los valores antes del 2013, corresponden al periodo comprendido entre1994-2012, tomados de la base de datos NHTSA.
Primero se calculó todas las longitudes de todas las variaciones anuales de la tasa de muertes por lesiones causadas por tránsito en Estados Unidos, con la ecuación 1. Para esta ecuación los valores del eje x que corresponde a la variación de cada año el cual toma valores de cero.
Halladas la tasa de longitudes con la ecuación 1, se calculó la probabilidad de cada tasa de longitud mediante la ecuación 2, que corresponde a los valores del primer espacio de probabilidad. Para ello se dividió la longitud para cada año entre la suma total de longitudes comprendidas del periodo comprendido entre 1994-2012. Seguidamente se halló la proporción entre la variación anual de cada una de las longitudes respecto al menor valor hallado en dicho periodo.
El segundo espacio de probabilidad se estableció a partir del calculó de la probabilidad de la tasa de muertes por lesiones causadas por tránsito para cada año reportada por la base de datos NHTSA, mediante la ecuación 3 dividiendo la tasa de muertes por lesiones causadas por tránsito reportado en un año entre la suma total de estas tasas de muerte en el periodo comprendido entre los años 1994-2012. Para determinar si existe un cargamiento en las probabilidades hacia valores específicos, al ser comparados los valores del segundo espacio de probabilidad con su valor esperado, se calculó la desviación media cuadrática de la tasa de muertes por accidente de tránsito en Estados Unidos.
Para predecir la tasa de muertes por lesiones causadas por tránsito para el 2013 en Estados Unidos, se estableció un tercer espacio de probabilidad, calculando primero el promedio aritmético de los valores de las longitudes halladas con la ecuación 1 para el período comprendido entre los años 2010-2012, para luego con este valor calcular la probabilidad de cada uno de estos tres periodos con la ecuación 2. Luego, el valor promedio de las longitudes probabilistas y la suma total de las tres longitudes comprendidas entre los años 2010-2012, fueron remplazados en la ecuación 5, incluyendo el valor de la longitud del año 2012; obteniendo como solución dos valores que corresponden a los rangos con los que determina la predicción.
El cuarto espacio de probabilidad compuesto por dos eventos disminución (D) y aumento (A) de muertes por lesiones causadas por tránsito, el cual permitió estudiar el comportamiento de períodos consecutivos de dos y tres años. El análisis hecho en este último espacio permite determinar cuál de los dos valores cuantitativos hallados con la ecuación 5 es más probable, y de este modo determinar con certeza el valor predictivo para el año 2013.
RESULTADOS
La tasa de muertes por accidente tránsito para el periodo comprendido entre los años 1994-2012 en Estados Unidos varió entre 10,42 y 15,91. Los valores de las longitudes halladas para este periodo variaron entre 0,05 y 1,39. Los valores de la probabilidad de la tasa de longitudes de muertes por accidente de tránsito se encontraron entre 0,008 y 0,212. Los valores de la proporción de las distancias respecto a la distancia mínima encontrada para este periodo estuvieron entre 1 y 27,80 (valores no se muestran). La probabilidad de la tasa anual de muertes por lesiones causadas por tránsito en Estados Unidos para este mismo periodo varió entre 0,039 y 0,060. La desviación media cuadrática para los valores de la tasa de muertes por accidente de tránsito osciló entre un rango de 0,009 y 0,091, encontrando que la diferencia entre estos últimos y el valor esperado varía en un rango de 0,031 y -0,031 (Tabla 1). El cálculo de probabilidades halladas para la tasa anual de muertes por lesiones causadas por tránsito en Estados Unidos y los valores de la desviación media cuadrática para el periodo comprendido entre los años 1994-2012, muestran que no son equiprobable, presentándose probabilidades cargadas que determinan la predicción para el año 2013 (tabla 1).

Tabla 1. Valores de la tasa de muertes por tránsito en Estados Unidos entre periodo comprendido en los años 1994-2012. Donde L: es la longitud de la tasa de muertes de tránsito, P(L): la longitud probabilista de la tasa de muertes de tránsito, (+/-) DMC: valores de la desviación media cuadrática de la tasa de muertes de tránsito.
Por otra parte, con el análisis realizado al tercer espacio de probabilidad que corresponde al periodo comprendido entre los años 2010-2012 de muertes por lesiones causadas por tránsito, así como la aplicación de la ecuación 5, se hallaron los dos valores de predicción para el año 2013 los cuales fueron de 10,44 y 11,8 (ver tabla3 y figura 1).
Para determinar el evento más probable para el año 2013 con relación a los aumentos (A) o disminuciones (D), se analizó la frecuencia y probabilidad de los valores consecutivos de los A o D (Tabla 2). Para ello, se analizó el tercer y cuarto espacio de probabilidades que contiene el número de posibles combinaciones entre A y D para un periodo de tres años consecutivos de muertes por LCT en Estados Unidos, encontrando que es más probable que haya una disminución de lesiones causadas por tránsito (ver tabla 3).

Tabla 2. Frecuencia y probabilidad de los aumentos y disminuciones consecutivas para el periodo comprendido entre los años 1994-2012, en relación a la tasa de muertes tránsito en Estados Unidos, donde V: representa el valor total de cada tipo de variación y P: la probabilidad de esta variación.

Tabla 3. Valores de los tres últimos años que corresponden a la tasa y L: longitud de muertes por lesiones causadas por tránsito para hacer la predicción del año 2013. Valor real tomado de la base de datos NHTSA.
Considerando como hecho más probable que haya una disminución, el establecimiento del valor predictivo fue realizado mediante el cálculo del promedio aritmético entre los dos valores predichos para el 2013 con la ecuación 5, tomando este resultado y el menor valor predicho para este año el cual fue de 10,44, nuevamente fueron promediados hallado como resultado 10,6, valor que al ser comparado con el reportado por NHTSA2 el cual corresponde a una tasa del 10,35 por cada 100.000 habitantes para el año 2013, se halló un porcentaje de acierto del 98 %. Al estudiar el espacio de probabilidad de aumentos y disminuciones se observa que las diferentes triplas presentan probabilidades que se diferencian, mostrando que por ejemplo la tripla DDD se presenta la mitad de las veces. (ver tabla 4).

Tabla 4. Número de posibles combinaciones de aumentos (A) y disminuciones (D) para un periodo de tres años consecutivos de muertes por tránsito en Estados Unidos, observada durante el periodo comprendido durante los años 1994-2012.
DISCUSIÓN
Este es el primer trabajo en el que se predice el número de muertes por LCT en Estados Unidos para el año 2013, analizando este comportamiento como si fuera una caminata al azar probabilista y el establecimiento de un espacio total de probabilidades. Se analizó el comportamiento de la dinámica de las longitudes probabilistas durante el periodo comprendido entre los años 2010-2012 respecto al promedio más probable, se consideró el comportamiento de aumentos y disminuciones durante el mismo periodo, estableciendo que el hecho más probable para el 2013 es que haya una disminución en la tasa de muertes por lesiones causadas por tránsito en Estados Unidos, logrando un 98% de predicción. Evidenciando así que la dinámica es un fenómeno determinista, contrariamente a la aleatoriedad e impredecibilidad que se le ha asociado convencionalmente.
Al analizar la dinámica del comportamiento de las LCT como una caminata al azar probabilista se pueden hacer proyecciones a futuro que contribuyan a optimizar los planes de acción orientados a la prevención y sensibilización de muertes por lesiones causadas por tránsito. También mediante la aplicación de esta metodología es posible hacer seguimientos del impacto que tienen los planes de acción para disminuir las lesiones causadas por tránsito, en el marco de la década de la seguridad vial (2011-2020) declarada por la WHO,14 que busca impulsar acciones que permitan obtener disminuciones del 50% en las muertes por causa de la violencia vial en los países más afectados.
Estudios realizados para evaluar el impacto que tienen las muertes por lesiones causadas por tránsito se han centrado en encontrar las causas, identificando por ejemplo el actor vial más vulnerable,26,27 como son los peatones, ciclista y motociclistas.18,27 Así mismo las lesiones más frecuentes por este tipo de accidentes.18 Por ejemplo, se ha establecido que, para el departamento de Valledupar, los motociclistas son los más afectados por las LCT, y se puede observar un continuo aumento en las LCT.28 En este trabajo se encontró un patrón matemático de estas lesiones y en la presente investigación se logran hacer predicciones a partir de patrones probabilistas. Otros estudios en cambio han identificado como posibles causantes de lesiones causadas por tránsito, los mecanismos de distracción del conductor,16 concluyendo después de analizar la literatura que trata del tema que los sistemas que integren contramedidas son los que pueden dar solución al problema.29
La dinámica de LCT a partir de la caminata al azar probabilista, permitió establecer predicciones a partir de una perspectiva acausal, considerando únicamente los aumentos y disminuciones propios de la dinámica, constituyéndose en una herramienta de ayuda para la toma de decisiones de salud pública, pues es más simple ya que permite abstraer los múltiples factores causales que has sido asociados a las LCT. Desde esta perspectiva acausal se han desarrollado metodologías para evaluar el comportamiento de epidemias, estableciendo predicciones del número de infectados de malaria y dengue en Colombia,21-24 estableciendo porcentajes de acierto de 90,4%22 para la epidemia de dengue y de 99,86% en la predicción de brotes semanales de malaria,21 permitiendo que los rangos de tiempo que usualmente son necesarios para el análisis de este tipo de dinámicas que son de 5 a 7 años29 se reduzca a tres semanas.
Órdenes matemáticos acausales se han encontrado en múltiples fenómenos de la medicina, permitiendo establecer predicciones en áreas como la cardiología de adulto,30 de mortalidad en pacientes de la Unidad de Cuidados Intensivo,31 en la fetal y neonatal, en inmunología y biología molecular, infectología. También, se han desarrollado metodologías de análisis y diagnóstico de imágenes de arterias coronarias, de células de cuello uterino y estructuras eritrocitarias.
CONCLUSIONES
El contexto en el que se desarrolló la metodología para evaluar la dinámica de muertes por lesiones causadas por tránsito en Estados Unidos, aparte de predecir la tasa de muertes por lesiones causadas por tránsito en un año especifico puede también predecir la tasa de muertes por lesiones causadas por tránsito de diferentes zonas de Estados Unidos, independiente de factores causales, análisis estadísticos y epidemiológicos.
Agradecimientos
Esta investigación hace parte del proyecto INV2288 financiado por la Universidad Cooperativa de Colombia.
Agradecemos a la Asociación Colombiana de Neurocirugía, especialmente a su presidente, el doctor Marco Fonseca y al doctor Germán Forero, Director de Investigaciones, por su apoyo a nuestras investigaciones
Conflictos de Interés
Los autores declaran no tener conflictos de interés.
REFERENCIAS
1. Spiegel M.R, Schiller J.J, Srinivasan RA. Probabilidad y estadística. Bogotá: Mc Graw Hill; 2003.
2. Feynman RP, Leighton RB, Sands M. Probabilidad. En: Feynman RP, Leighton RB, Sands M. Física. Wilmington: Addison-Wesley Iberoamericana, S. A; 1964; p. 6-1, 6-16.
3. Laplace P. Ensayo filosófico sobre las probabilidades. Barcelona: Altaza, 1995. p. 12-15
4. Blanco L. Probabilidad. 1a ed. Bogotá: Unibiblos; 2004
5. Pearson K. The Problem of the Random Walk. Nature. 1905; 72: 294.
6. Cattoni D, Ozu M, Chara O. Ruidos en la naturaleza An AFA. 2004; 16: 294-99. Disponible en: https://www.academia.edu/30624724/Ruidos_en_La_Naturaleza
7. Van Kampen N.G. Stochastic Processes in Physics and Chemistry. 3a ed. North-Holland, Amsterdam; 2007.
8. Redner S.A Guide to First-Passage Process. Cambridge. Cambridge University Press; 2001.
9. Goel N.S, Richter N. Stochastic Models in Biology. 1a ed. New York, Academic Press; 1974.
10. Doi M, Edwards S. The Theory of Polymer Dynamics. 1a ed. Oxford, Clarendon Press; 1986
11. De Gennes P.G. Scaling Concepts in Polymer Physics. Ithaca, N.Y: Cornell University Press; 1979.
12. Risken H, Frank T. The Fokker–Planck Equation. 2a ed. Berlin, Springer; 1984.
13. Weiss, G. Aspects and Applications of the Random Walk. Amsterdam: North-Holland, 1994.
14. World Heath Organization. Global status report on road safety. Luxembourg City Luxembourg, 2013.
15. Organización Mundial de la Salud. Informe sobre la situación mundial de la seguridad vial: es hora de pasar a la acción. Ginebra, Suiza, 2013 [Citado el 1 Diciembre 2018]. Disponible en: www.who.int/violence_injury_prevention/publications/road_tra€c/en/index.html.
16. Centers for Disease Control and Prevention (CDC). Mobile device use while driving--United States and seven European countries, 2011. [Ciado 17 dic 2018]. Disponible en: https://www.cdc.gov/mmwr/preview/mmwrhtml/mm6210a1.htm
17. Híjar M. Utilidad del análisis geográfico en el estudio de las muertes por atropellamiento. Salud publica Mex. 2000; 42:188-193. Disponible en: https://www.scielosp.org/article/spm/2000.v42n3/188-193/
18. Dultz L, Foltin G, Simon R, Wall S, Levine D, Bholat O, et al. Vulnerable roadway users struck by motor vehicles at the center of the safest, large US city. Journal of Trauma and Acute Care Surgery. 2013; 74(4): 1138–1145. Disponible en: https://insights.ovid.com/pubmed?pmid=23511157
19. Denning G, Harland K, Ellis D, Jennissen C. More fatal all-terrain vehicle crashes occur on the roadway than off: increased risk-taking characterises roadway fatalities. Inj Prev 2013; 19:250-256. Disponible en: https://injuryprevention.bmj.com/content/19/4/250
20. Nathens A, Jurkovich G, Cummings P, Rivara F, Maier R. The Effect of Organized Systems of Trauma Care on Motor Vehicle Crash Mortality. JAMA. 2000; 283(15):1990-1994. Disponible en: https://jamanetwork.com/journals/jama/fullarticle/192607
21. Rodríguez J. Método para la predicción de la dinámica temporal de la malaria en los municipios de Colombia. Rev Panam Salud Pública 2010; 27(3):211-218. Disponible en: http://iris.paho.org/xmlui/bitstream/handle/123456789/9708/a08v27n3.pdf?sequence=1&isAllowed=y
22. Rodríguez J, Correa C. Predicción temporal de la epidemia de dengue en Colombia: dinámica probabilista de la epidemia. Rev. Salud pública. 2009; 11 (3): 443-453. Disponible en: https://revistas.unal.edu.co/index.php/revsaludpublica/article/view/37041/39046
23. Rodríguez J. Dinámica probabilista temporal de la epidemia de malaria en Colombia. Rev Fac Med. 2009; 17(2):214-221. Disponible en: http://www.scielo.org.co/pdf/med/v17n2/v17n2a05.pdf
24. Rodríguez J, Prieto S, Farjardo E, Correa C, López F, Castro J, Soracipa Y. Predicción de la dinámica temporal de egresos hospitalarios por obesidad en niños y jóvenes en Estados Unidos. Rev Chil Nutr 2015; 42(4):345-350. Disponible en: http://www.redalyc.org/toc.oa?id=469&numero=43554
25. Otte D, Jänsch M, Haasper C. Injury protection and accident causation parameters for vulnerable road users based on German In-Depth Accident Study GIDAS. Accident Analysis & Prevention. 2012; 44(1): 149-153. Disponible en: https://www.sciencedirect.com/science/article/abs/pii/S0001457510003830
26. Rodríguez J, Peñalosa R, Ariza L, Flórez C, Armindo F, Montoya S, et al. Factores de riesgo asociados a lesiones causadas por el tránsito y propuestas de intervenciones para el contexto colombiano. 1a ed. Universidad Javeriana. Bogotá: Ecoe ediciones. 2015.
27. Rodríguez JM, Peñaloza RE, Moreno Montoya J. Road traffic injury trends in the city of Valledupar, Colombia. A time series study from 2008 to 2012. PLoS ONE. 2015; 10(12): e0144002. Disponible en: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0144002
28. Young K, Salmon P. Examining the relationship between driver distraction and driving errors: A discussion of theory, studies and methods. Safety Science. 2012; 50(2):165-174. Disponible en: https://www.sciencedirect.com/science/article/pii/S092575351100155X
29. Bortman M. Elaboración de corredores o canales endémicos mediante planillas de cálculo. Rev Panam Salud Publica. 1999; 5(1):1–8. Disponible en: https://scielosp.org/pdf/rpsp/1999.v5n1/1-8/es
30. Rodríguez J, Prieto S, Correa C, Bautista J, Velasco A, Méndez, et al. Mathematics physical assessment of cardiac dynamics based on theory of probability and proportions of entropy in the intensive care unit for patients with arrhythmia. J Nucl Med Radiat Ther. 2015;6:4. Disponible en: https://www.omicsonline.org/2155-9619/2155-9619.S1.002-012.pdf
31. Rodríguez J. Dynamical systems applied to dynamic variables of patients from the intensive care unit (ICU): Physical and mathematical mortality predictions on ICU. J. Med. Med. Sci. 2015; 6(8): 102-108. Disponible en: http://dx.doi.org/10.14303/jmms.2015.115
Recibido: 30 Octubre 2020
Aceptado: 30 Enero 2021
Javier Rodríguez-Velásquez1*, María Alejandra González-Bernal2, Adiela Ruiz-Gómez3, Esmeralda Guzmán-de la Rosa4, Daniel Pallejá-Lopez5, Freddy Barrios-Arroyave6, Oscar Valero-Alvarado7, Ribká Soracipa-Muñoz8, Nathalia López-Sardoth9, Jorge Rodríguez-Hernandez10
1 MD. Director del Grupo Insight. Asociación Colombiana de Neurocirugía. Bogotá, Colombia.
2Odontóloga. Docente Universidad Cooperativa de Colombia. Bogotá, Colombia.
3Odontóloga. Docente Universidad Cooperativa de Colombia. Bogotá, Colombia.
4 MD. Investigadora Grupo Insight. Bogotá, Colombia.
5 Matemático. Investigador Grupo Insight. Bogotá, Colombia.
6 MD. M.Sc. Fundación Universitaria Autónoma de las Américas. Pereira, Colombia.
7 MD. M.Sc. Infecciones y Salud en el Trópico. Epidemiólogo. Escuela de Ciencias de la Salud. Universidad Nacional Abierta y a Distancia. Bogotá, Colombia.
8 Lic. Física. Investigadora Grupo Insight. Asociación Colombiana de Neurocirugía. Bogotá, Colombia.
9 Estudiante de física. Universidad de Los Andes. Investigadora Grupo Insight. Centro de Investigaciones Clínica del Country. Bogotá, Colombia.
10 MD M.Sc. FETP PhD. Instituto de Salud Pública. Pontificia Universidad Javeriana. Bogotá, Colombia.
Corresponding author: Javier Rodriguez-Velasquez: Cel: +573134057252, Cra. 79B N° 51-16 Sur. Int. 5. Apto. 102, Kennedy, Bogotá D.C., Colombia. Teléfono: 4527541; Correo electrónico: [email protected]
