2023.08.03.103

Files > Volume 8 > Vol 8 No 3 2023

Preview / Index / Next

Modelamiento matemático del efecto del retraso del tratamiento sobre la resistencia del VIH a drogas en hombres que tienen sexo con hombres ecuatorianos.

Mathematical modeling of the effect of treatment delay on HIV drug resistance in Ecuadorian Men Seeking Men

Gabriel Morey-León^1,*

, Jesús Vega-Lugo²

, James Humberstone³

, Manuel Gonzalez-Gonzalez⁷

, Emmanuel J. Morales-Butler⁴

, Marlio Paredes⁵

, Anuj Mubayi⁵

, Padmanabhan Seshaiyer⁶

, Patricio Vega-Luzuriaga⁷

¹Facultad de Ciencias de la Salud, Universidad Espiritu Santo. [email protected].

² Departamento de Ciencias Naturales, Universidad Sagrado Corazón, Puerto Rico.

³ Instituto de Ciencias, Tecnología e Innovación, Universidad Francisco Gavidia, El Salvador.

⁴ Departamento de Matemáticas y Físicas, Universidad de Puerto Rico en Cayey, Puerto Rico.

⁵ Simon A. Levin Mathematical, Computational and Modeling Sciences Center, Arizona State University, Arizona.

⁶ Departamento de Ciencias Matemáticas, George Mason University, Virginia.

⁷Instituto de Nacional de Investigación en Salud Pública "Leopoldo Izquieta Pérez", Guayaquil, Ecuador.

*Correspondencia: [email protected], Tel. 0997720241

Available from: http://dx.doi.org/10.21931/RB/2023.08.03.103

RESUMEN

Uno de los principales desafíos actuales de salud pública incluye proporcionar una terapia antirretroviral eficaz contra el VIH centrada en la relación entre el tratamiento y la prevalencia de la resistencia a los medicamentos. Aunque está bien documentado que las tasas de VIH/SIDA entre los hombres que tienen sexo con hombres (HSH) tienden a ser más altas que en la población general, poco se sabe sobre la tasa de prevalencia entre los HSH en Ecuador. El objetivo de este estudio fue evaluar mediante modelamiento matemático los efectos del retraso del tratamiento sobre los cambios en la prevalencia de casos infecciosos y farmacorresistentes en una población de HSH positiva a VIH. Un nuevo modelo matemático que incorpora una distribución no exponencial del periodo infeccioso y una cobertura de tratamiento variable fue desarrollado y analizado numéricamente para capturar la dinámica de transmisión del VIH. Nuestros resultados mostraron que la tasa de transmisibilidad y la efectividad del tratamiento tienen una influencia significativa en la predicción del modelo a partir del análisis global de incertidumbre y sensibilidad. Este trabajo sería el primer modelo matemático para abordar la dinámica del VIH entre los HSH en Ecuador.

Palabras claves: VIH, Modelamiento matemático, HSH.

ABSTRACT

One of the major current public health challenges includes providing effective HIV antiretroviral therapy focused on the relationship between treatment and prevalence of drug resistance. Although it is well documented that the rates of HIV/AIDS among Men Seeking Men (MSM) tend to be higher than in the general population, little is known about the prevalence rate among MSM in Ecuador. The aim of this study was to evaluate, through mathematical modeling, the effects of delaying treatment on changes in the prevalence of infectious and drug resistance in Ecuadorian HIV-positive Men Seeking Men populations. A new mathematical model that incorporates a non-exponentially distributed infectious period and variable treatment coverage is developed and analyzed numerically to capture the HIV transmission dynamics in Ecuador. Our results showed that rate of transmissibility and treatment effectiveness have significant influence on the model’s prediction from the global uncertainty and sensitivity analysis. This work it would be the ﬁrst mathematical model to address HIV dynamics among Men seeking Men in Ecuador.

Keywords: HIV, Mathematical modeling, MSM.

INTRODUCTION

La epidemia del Virus de Inmunodeficiencia Humana (VIH-1) ha estado marcada por significantes éxitos y fallas en investigaciones biomédicas y conductuales. Para finales del 2021, a nivel mundial un promedio de 38,4 millones de personas vivían con el VIH, de estos, el 46% conocía su estatus de seropositividad, mientras el 75% recibía terapia antirretroviral (ART).^1,2 En Latinoamérica, la prevalencia estimada del VIH-1 en adultos de 15 a 49 años es de 0,5% [rango: 0,3% - 0,6%] la cual se ha mantenido prácticamente estable desde el año 2000,¹ sin embargo, la epidemia globalmente se está expandiendo entre hombres que tiene sexo con hombres (HSH) independientemente del país debido a las diferentes prácticas sexuales.^3–6 Varios autores han mostrado un incremento de los niveles de prevalencia en rangos que van del 6 al 20% entre la población infectada de HSH. Alrededor del 50% de infecciones por VIH-1 son asumidas como resultado de sexo entre hombre sin protección.^7–13

En Ecuador, 47.000 [rango: 42.000 – 53.000 casos] personas (entre adultos y niños) vivían con el VIH-1 en 2021, representando una tasa de prevalencia de 0,4% entre adultos de 15 a 49 años,¹⁴ siendo las provincias de las costa el epicentro de la epidemia en el país.¹⁵ Aunque están bien documentadas las tasas de VIH/SIDA entre HSH mundialmente, muy poco es conocido sobre las tasas de prevalencia entre la población HSH ecuatoriana.^16,17 La población de HSH representa el 17% entre las poblaciones con alto riesgo de VIH analizadas en el país.¹⁸ Sin embargo, varios estudios muestran diferencias en las prevalencias yendo de 10,5% en el noroeste del Ecuador,¹⁹ 11% o 14,5 en Quito,^20,21 mientras que en Guayaquil de 11.3% entre 2011 - 2012²² a 27.8%.²¹

Modelamientos matemáticos combinado con mediciones experimentales han producido importantes datos sobre la patogénesis y potenciaron un progreso en el entendimiento de la infección del VIH-1. Modelos empleados para el estudio de la infección del VIH-1 han incluido variables como carga viral e infectividad, latencia y reservorio, respuesta a la ART, evolución de la resistencia a drogas, entre otras.^23–35 Más aun, algunos modelos han sido aplicados para estimar la diseminación del VIH-1 sobre la población humana, especialmente HSH,^3,36–45 quienes estarían envueltos en la dispersión de la enfermedad entre las poblaciones de riesgo. El desafío de este tipo de modelamientos son los datos incompletos de la población de HSH debido al estigma social y discriminación. Esta limitación hace bastante complejo realizar predicciones exactas sobre la incidencia de VIH-1 entre esta población. Sin embargo, los modelos matemáticos nos permiten explorar los resultados bajo diferentes escenarios y determinar las posibles consecuencias de tener o no alguna medición controlada. En Latinoamérica muy pocos estudios se han realizado evaluando población HSH, y casi siempre están asociados a la evaluación del costo-beneficio de la profilaxis preexposición,⁴⁶ en ese contexto, se ha utilizado modelamiento matemático para evaluar el impacto en población HSH en Perú,^36,47 seguido por Estados Unidos,⁴⁸ Brasil.⁴⁹ El objetivo de nuestro estudio fue evaluar mediante modelamiento matemático el impacto del retraso del tratamiento contra el VIH sobre los cambios en la prevalencia de infección y resistencia a drogas en HSH e identificar el principal factor que afecta la dispersión entre ellos. Nos enfocamos sobre la dinámica del transmisión del VIH en Ecuador, donde se reporta que la prevalencia en HSH está entre 10 y 27%, evaluando diferentes estrategias de tratamiento con la finalidad de identificar la más eficiente en mantener la menor cantidad de población infectiva y resistente.

MATERIALES Y METODOS

Nuestro modelo matemático fue propuesto considerando las tasas de transmisión, infección, mortalidad y efectividad del tratamiento, adaptándose a un modelo determinístico tipo SEIR(Sensibles, Expuestos, Infectados, Recuperados),⁵⁰ lo cual permitió ajustar la dinámica del VIH-1 entre los diferentes estados de la infección viral y las diferentes líneas de tratamiento. El modelo se representa esquemáticamente en la figura 1, describiendo el proceso natural de una infección de VIH e incluye los efectos del tratamiento, así como las tasas a las cuales la resistencia se desarrolla durante el tratamiento.

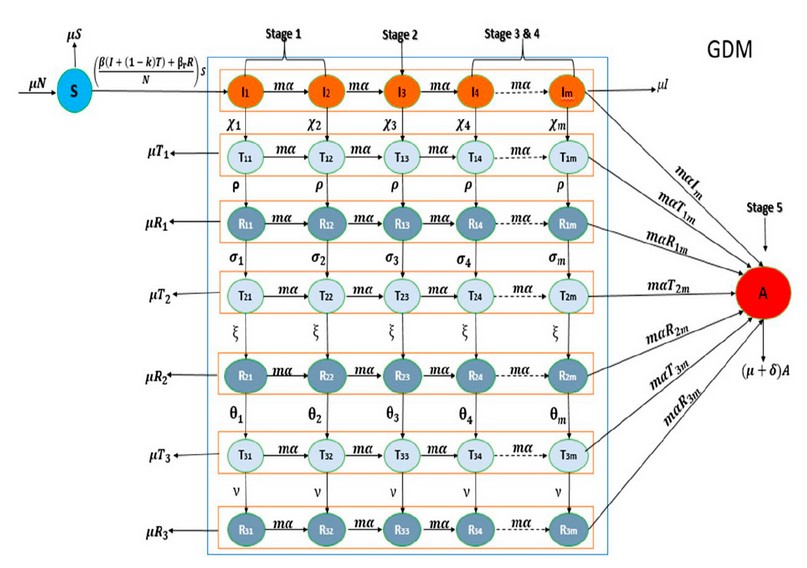
Figura 1. Diagrama esquemático para los estadios de progresión del VIH, incluyendo compartimientos para Susceptible (S), Tratados (T), Resistentes (R), y SIDA (A).

Aquí asumimos una distribución gamma (especialmente Erlang) del periodo infecciosos para las cuatro etapas de la enfermedad como se ha mostrado en estudios previos.⁵¹ En el desarrollo de nuestras ecuaciones del modelo, consideramos el tamaño de la población total, así como, las tasas a las cuales los individuos se mueven entre sub-compartimientos como constantes, así como una adherencia al tratamiento del 100% de todos los individuos tratados y que los individuos tratados pueden infectar susceptibles dependiendo de la efectividad del tratamiento (κ). Para los casos en los cuales un individuo susceptible se infecta con cepas resistentes del virus, por ejemplo, a partir de individuos del compartimiento R también fue considerado. Para estos casos, se consideró que estos individuos son parte del grupo de infectados (I). Esto es debido que al tiempo del diagnóstico no hay manera de conocer si el individuo infectado es resistente al tratamiento. N es la población total acorde a N=S+I+T+R+A. El correspondiente modelo de ecuaciones diferenciales ordinarias no lineares (ODE) es proporcionado como sigue:

Individuos susceptible se infectan con el virus VIH-1 a través de un contacto exitoso con individuos en los compartimientos I, T y R (parámetro de transmisión β).

Individuos infectados con cepas sensibles pueden moverse a clase tratada a una tasa per capita, χ, donde χ es la tasa de movimiento de las estrategias de tratamiento de interés.

Individuos tratados pueden desarrollar resistencia (falla terapéutica) a una tasa constante per capita ρ

Si mutaciones se generan en el genoma viral, los individuos infectados pueden moverse a la segunda clase de tratados a una tasa constante per capita σ

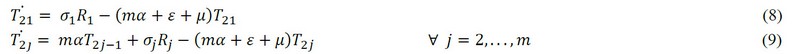
Individuos tratados con la segunda estrategia pueden desarrollar resistencia (falla terapéutica) a una tasa constante per capita ξ.

Individuos infectados que desarrollaron resistencia a la segunda estrategia pueden moverse a la tercera clase de tratados a una tasa constante per capita θ

Individuos infectados que desarrollan resistencia a la tercera estrategia pueden moverse a la tercera clase de tratados a una tasa constante per capita ν

Individuos de cada uno de los siete niveles de infección pueden moverse a SIDA a una tasa per cápita mα, donde m es el parámetro de forma de la distribución gamma asociada con el periodo infeccioso, la cual está representada por el número de sub-compartimientos en nuestro modelo, mα es la tasa de movimiento horizontal en los estados de la enfermedad. Finalmente, individuos en cada uno de los siete niveles de infección (Infectado, Tratados 1, 2 y 3, Resistentes 1, 2, y 3) y SIDA dejan el sistema, tanto por la muerte o recuperación de su inmunidad a una tasa per cápita constante µ.

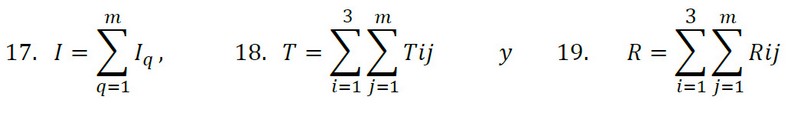
Donde

La definición de variables y todos los parámetros utilizados en nuestro modelo son provistos en la tabla 1.

Tabla 1. Definición de variables de estadio y parámetros del modelo.

Estimación de parámetros

Para el cálculo de los sub-compartimientos (m) y el parámetro de forma (ω) de la distribución gamma, empleamos la media y la varianza para el periodo infeccioso en HSH, siendo 136,83 meses y 429,025 meses, respectivamente acorde a.⁵² Con estos datos calculamos m=43 y α = 0,028848 años^-1. Para la estimación del desarrollo de resistencia en los individuos de la primera (ρ), segunda (ξ) o tercera (ν) línea del tratamiento, primero asumimos que la tasa a la cual los individuos tratados desarrolla resistencia es constante entre los tres esquemas de tratamiento. Luego, empleamos el número de individuos positivos VIH-1 que desarrollaron mutaciones relacionadas a resistencia (92 individuos positivos). Para determinar las tasas de ρ, ξ y ν, dividimos el número de individuos resistentes (92) para los 3.546 casos positivos totales de VIH en 2014. Se empleó datos de ONUSIDA(1) para estimar la tasa a la cual los individuos infectados reciben tratamiento (χ), siendo de 52 de cada 100 personas infectadas en Ecuador y de 58 de cada 100 en Latinoamérica,⁵³ para convertir este número en un ratio, empleamos la población total de casos positivos VIH en 2014.

Definición de estrategias de tratamiento.

Antes de establecer las estrategias de tratamiento, calculamos el promedio de tiempo que un individuo podría pasar en cada sub-compartimiento. Para esto, dejamos el promedio de vida de un individuo infectado por VIH-1 en 20 años para 2014, teniendo en cuenta que la supervivencia de una persona seropositiva está influenciado acorde con la atención en salud oportuna, recepción constante del tratamiento y los hábitos cotidianos,^54–56 y lo dividimos para el parámetro de forma m. Con esta información definimos tres intervalos de tiempo (categoría uno, 48 semanas, categoría dos, 24 semanas y categoría tres, 960 semanas) en las cuales los individuos reciben tratamiento. Luego, consideramos cinco estrategias de tratamiento considerando no adherencia (1 – 2) y retraso (3 – 5), las cuales se encuentran representada en la Tabla 2.

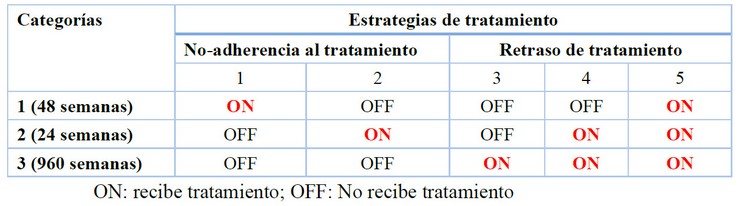
Tabla 2. Estrategias de tratamiento para los grupos de no adherencia y retraso del tratamiento, considerando las tres diferentes categorías: 1 (48 semanas), 2 (24 semanas) y 3 (960 semanas).

Para la primera estrategia, el paciente recibe tratamiento solo por las primeras 48 semanas después de la infección seguido del abandono del mismo; en la segunda estrategia, después de 48 semanas de infección, el paciente es detectado y recibe tratamiento por 24 semanas y luego abandona este después de esta en la semana 72 de infección; en la tercera estrategia, el retraso de recibir tratamiento fue por 72 semanas después de la infección y luego iniciado en la semana 73 y continuado hasta el final; para la cuarta estrategia, el retraso en recibir tratamiento fue de 48 semanas, se inicia en la semana 49 y continuado hasta el final; y en la quinta estrategia consideramos un caso hipotético en donde el tratamiento es recibido desde el primer momento de la infección (sin retraso).

Análisis de Incertidumbre global y sensibilidad.

Análisis de incertidumbre global y sensibilidad permite cuantificar como los cambios en los valores de los parámetros de ingreso alteran los valores de las variables en los resultados.⁵⁷ Analizamos la variabilidad de los parámetros β, βr, κ, χ, α, µ, ρ, ξ, ν y su efecto predictivo dentro de nuestro modelo, mediante el análisis de incertidumbre global y sensibilidad vía Latin Hypercube Sampling (LHS) y Partial Rank Correlation Coefﬁcient (PRCC).

Una función de distribución de probabilidad (PDF, por su denominación en inglés) fue asignada a cada parámetro empleado en el modelo y una distribución de uniformidad Unif (a, b) con parámetros a y b para cada parámetro de ingreso fue empleada, donde a es el valor mínimo y b es 2mean value - min value. Los valores empleados en el análisis se encuentran descritos en la Tabla 5.

El análisis de sensibilidad para cada estrategia de tratamiento fue realizado para determinar el efecto de todos los parámetros con respecto al modelo, los niveles de significancia para el análisis fueron 0,001, 0,01, 0,05, 0,1 en los cuales el parámetro podría tener influencia sobre la estrategia de tratamiento.

Análisis numérico

Para el análisis numérico, empleamos los valores estimados de los parámetros y obtenidos de investigaciones previas, resumidas en la tabla 3.

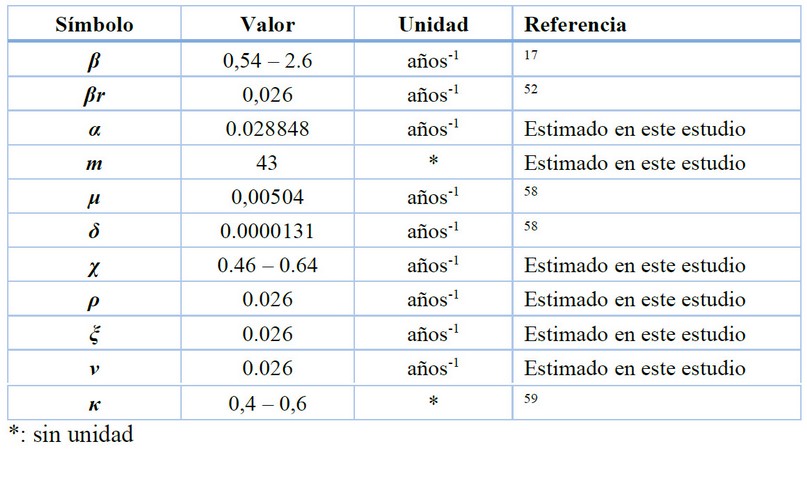
Tabla 3. Parámetros y valores estimados o seleccionados para simulaciones de nuestro modelo.

RESULTADOS

Los parámetros de distribución uniforme Unif (a, b) calculados, utilizados en el análisis de incertidumbre y sensibilidad y descriptivos estadísticos empleados para el análisis de incertidumbre para los parámetros β, βr, κ, χ, α, µ, ρ, ξ, ν del modelo, son mostrados en la tabla 4 y 5.

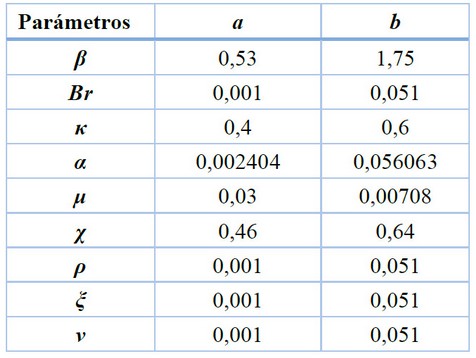
Tabla 4. Parámetros de distribución uniforme para los análisis de incertidumbre y sensibilidad

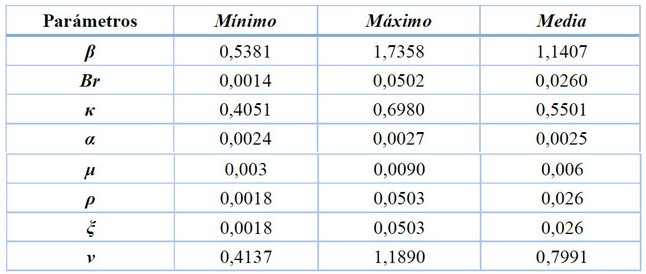
Tabla 5. Descriptivos estadísticos para el análisis de incertidumbre

A partir del análisis de incertidumbre global y sensibilidad se obtuvo que la tasa de infección (β) y la eficiencia del tratamiento (κ) son los parámetros que más influencian sobre las diferentes estrategias (nivel de significancia de 0,001) representados en el PRCCs proporcionales (figura 3, tabla 6). Denotándose que β tiene una alta influencia sobre la estrategia 2 y una baja influencia en la estrategia 4, pero κ tiene una influencia inversamente proporcional sobre los resultados de cada estrategia, teniendo una fuerte influencia con la estrategia 2 mientras una baja influencia sobre la estrategia 1. Con los resultados de los análisis de sensibilidad se puso especial atención sobre la tasa de infección (β) y la eficiencia del tratamiento (κ) para evaluarlos en nuestras simulaciones.

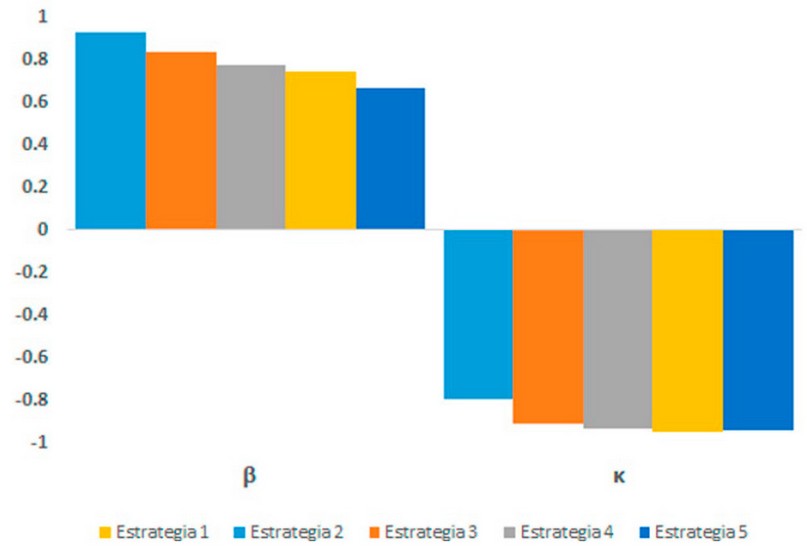
Figura 2. Ploteo de los resultados del análisis de Sensibilidad para cada estrategia. Nótese que β tiene una influencia proporcional, pero κ tiene una influencia inversamente proporcional sobre los resultados de cada estrategia.

Durante la simulación de evaluación del efecto de β sobre las estrategias de tratamientos con retraso (3 y 4), observamos una tendencia donde el inicio del tratamiento, en los estadios tardíos produce más casos infecciosos, pero reduce los casos resistentes, mientras que el inicio temprano del tratamiento (estrategia 5) produce menos casos infecciosos pero mayor número de casos resistentes.

Tabla 6. Resultados de los PRCCs para tasa de transmisión (β) y efectividad del tratamiento (κ).

Para poblaciones infecciosas con β = 0.54 y 2.6 la estrategia cuatro produce menos casos infecciosos que la estrategia tres (0,328 para β=0,54 y 0,297 para β=2,6). Para poblaciones resistentes con β= 0.54 y 2.6 observamos que la aparición de poblaciones resistentes incrementa para todas las estrategias con retraso, sin embargo, la estrategia tres produce menos casos resistentes que la estrategia cuatro (0,05 para β=0,54 y 0,07 para β=2,6); mientras que la incorporación de una estrategia temprana produce un mayor número de casos resistentes (figura 4a).

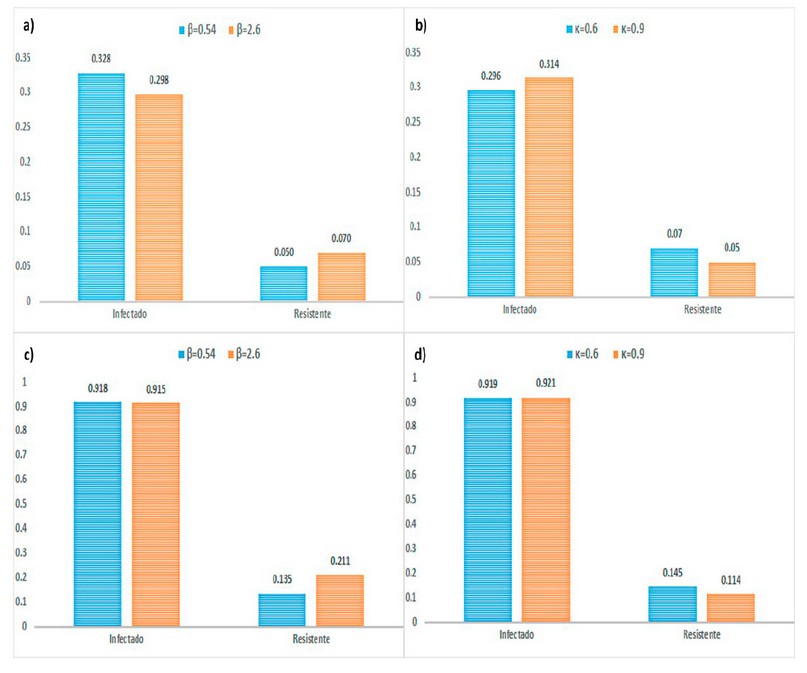
Figura 3. Ploteo de los resultados de simulaciones de las estrategias 3 vs 4. Nótese los resultados de β y κ para estrategias con retraso del tratamiento (paneles a y b) y no adherencia al tratamiento (paneles c y d).

Cuando se evaluó el efecto de κ, observamos que cuando se utilizó un κ = 0.6, retrasos similares para alcanzan el punto epidémico se obtuvieron en todas las estrategias. En las poblaciones infecciosas tanto con κ = 0.6 y 0.9 la estrategia cuatro produce menos casos infecciosos que la estrategia tres (0,296 para κ=0,6 y 0,314 para κ=0,9). En poblaciones resistentes bajo los mismos valores de κ = 0.6 y 0.9 observamos que el inicio del crecimiento de la población resistente para todas las estrategias tuvo retrasos, y la estrategia tres produce menos casos resistentes que la estrategia cuatro (0,07 para κ=0,6 y 0,05 para κ=0,9), manteniéndose la estrategia cinco como la que mayor número de casos resistentes produce (figura 4b).

En el caso de las estrategias sin adherencia, al analizar β la estrategia uno produce menos casos infecciosos que la estrategia dos (0,918 para β=0,54 y 0,915 para β=2,6); así mismo la estrategia uno reduce el número de individuos resistentes comparados con la estrategia dos (0,135 para β=0,54 y 0,211 para β=2,6). Sin embargo, al analizar κ, observamos que la estrategia dos produce menos casos infecciosos que la estrategia 1, siendo κ=0,9 la más adecuada (0,921 para κ=0,9 y 0,919 para κ=0,6); en el caso de los resistentes se pudo observar que κ=0,6 genero menos casos (0,145) que κ=0,9 (0,114) (figura 4c y 4d).

DISCUSIÓN

El presente estudio evalúa mediante simulación matemática los efectos del retraso del tratamiento sobre los cambios en la prevalencia de casos infecciosos y farmacorresistentes en una población de HSH positiva a VIH en Ecuador. Las simulaciones basadas en computadoras sobre modelos ODE para la epidemia del VIH mostraron que el tratamiento sin reducción de comportamiento de riesgo puede incrementar los casos de individuos infecciosos.^60,61 Sin embargo, sea demostrado que las tasas de incidencia de VIH disminuirán a medida que más personas infectadas tengan acceso a la terapia antirretroviral (TARGA),^62–64 pero este beneficio en la salud pública ocurre si los niveles de comportamiento de riesgo no aumentan.

Nuestros resultados numéricos basados en simulaciones ODE con modelado del periodo infeccioso distribuido no exponencialmente mostró que, si el TARGA es introducido en periodos tempranos de la infección, reduciría el número de individuos infecciosos, pero al mismo tiempo incrementa la cantidad de individuos resistentes. Sin embargo, si el comportamiento de riesgo incrementa (altos valores de β), la proporción de individuos infecciosos incrementa aún más. Por otro lado, la estrategia tres (retrasado por 72 semanas después de la infección y luego iniciado en la semana 73 y continuado hasta el final) produce menos cantidad de individuos resistentes, pero incrementa considerablemente la población de infecciosos.

Simulaciones de ODE mostraron que la combinación entre el tratamiento antirretroviral y el decrecimiento del comportamiento de riesgo es una estrategia promisoria contrata la epidemia del VIH.^60,65 En nuestro modelo, obtuvimos similares resultados cuando reducimos β con una alta cobertura (0,9), siempre y cuando la efectividad del tratamiento incremente de 0,9 a 0,95. Reducir β implica una disminución en el comportamiento de riesgo de los individuos, lo cual ha mostrado presenta un impacto positivo dentro de la disminución de casos infecciosos^66,67 lo cual podría ser posible con una detección temprana y conocimiento de la dispersión de la enfermedad.

En estrategias de no adherencia al tratamiento, la estrategia uno es más eficiente, reduciendo el número de individuos infectados (91,8%) que la estrategia dos; sin embargo, la estrategia dos produce menos casos resistentes (13,5% para β y 11,4% para κ). Entre las estrategias con retraso, la estrategia sin retraso (cinco) reduce en 96% el número de individuos infectados comparados con la estrategia tres; pero la estrategia tres es mucho mejor disminuyendo el número de individuos resistentes que la estrategia cinco (11% para β y 13% para κ).

Nuestro estudio presenta varias limitaciones, primero, se asume la adherencia del 100%, sin considerar las deserciones que ocurren en la realidad; segundo, el limitado acceso a información exacta de casos resistentes, así como de las mutaciones predominantes, basados en el poco análisis de resistencia, podrían impactar en los resultados de nuestro modelo por lo cual deberían analizarse a posteriori; tercero, al considerarse solo datos del año 2014 no se puede evidenciar que existan cambios acorde a las políticas de salud que hayan sido aplicadas en la mejora de la detección y adherencia al tratamiento en años posteriores. Cuarto, no se conoce por completo las diferentes conductas de riesgo que puedan practicar la población HSH, debido a su limitado acceso por prejuicios, discriminación y estigmatización.⁶⁸

CONCLUSIÓN

A nuestro conocimiento, este sería el primer modelo matemático que direcciona la dinámica del VIH entre HSH en Ecuador, el cual podría ser tomado de base para ampliar estudios que puedan simular diferentes panoramas de la enfermedad en poblaciones de riesgo del país y plantear propuestas de acción que mejoren el acceso a tratamiento oportuno y concienciar sobre las conductas de riesgo. Posteriores modelos y simulaciones deberían considerar uso de barreras físicas (condones) y el uso de drogas inyectables (UDI) en la dinámica del VIH sobre otras poblaciones de riesgo, además de evaluar el impacto de las mutaciones más comunes asociadas con la resistencia, el retraso del diagnóstico y la carga viral sobre los diferentes esquemas de tratamiento en Ecuador.

En conclusión, nuestro estudio permitió modelar el impacto del retraso en la recepción del tratamiento sobre una población HSH, VIH positiva evidenciando que cambios en el comportamiento de riesgo disminuyen la tasa de transmisibilidad, por lo cual es necesario concienciar sobre las conductas sexuales en las poblaciones de riesgo como la HSH, transfemeninas y realizar los esfuerzos necesarios para incrementar la eficacia en la recepción de tratamiento con el objeto de mantener la dispersión de la enfermedad en los niveles más bajos posibles.

Supplementary Materials: No Aplica.

Author Contributions: Conceptualización, G.M.L., E.M.B.; Desarrollo de sistema de ecuaciones, G.M.L., J.V.L., J.H.; Validación de sistema de ecuaciones y simulaciones, E.M.B., M.P., A.M.; Análisis Global de sistema, E.M.B., M.P., A.M., P.S.; Escritura y preparación del manuscrito, G.M.L., J.V.L., J.H, M.G.G.PV.; Revisión final del manuscrito, E.M.B., M.P., A.M., P.S.PV. Todos los autores han revisado y están de acuerdo con la versión publicada del manuscrito.

Funding: Esta investigación fue parcialmente soportada mediante el fondo de la National Science Foundation (DMS1263374), la oficina de la Presidencia y del Rectorado de la Universidad del Estado de Arizona (Arizona State University, ASU)

Institutional Review Board Statement: No Aplica.

Informed Consent Statement: No Aplica.

Data Availability Statement: No Aplica.

Acknowledgments: Agradecemos al Programa de Verano REU (Research Experience for Ungraduate) en el Centro Ciencias de Modelamiento Computacional y Matemático “Simon A Levin (SAL MCMSC) en la Universidad del Estado de Arizona (Arizona State University, ASU), por permitirnos desarrollar la presente investigación durante el curso asistido.

Conflicts of Interest: Los autores no declaran conflicto de interés.

REFERENCIAS

1. ONUSIDA. IN DANGER: UNAIDS Global AIDS Update 2022 [Internet]. Geneva, Switzerland: Joint United Nations Programme on HIV/AIDS; 2022 [citado 11 de abril de 2023] p. 376. Disponible en: https://www.unaids.org/es/Homepage

2. WHO. HIV data and statistics [Internet]. 2023 [citado 11 de abril de 2023]. Disponible en: https://www.who.int/teams/global-hiv-hepatitis-and-stis-programmes/hiv/strategic-information/hiv-data-and-statistics

3. Beyrer C. Global Prevention of HIV Infection for Neglected Populations: Men Who Have Sex with Men. Clin Infect Dis. 15 de mayo de 2010;50(Supplement_3):S108-13.

4. Tan RKJ, O’Hara CA, Koh WL, Le D, Tan A, Tyler A, et al. Delineating patterns of sexualized substance use and its association with sexual and mental health outcomes among young gay, bisexual and other men who have sex with men in Singapore: a latent class analysis. BMC Public Health. 31 de mayo de 2021;21:1026.

5. He S, Song W, Guo G, Li Q, An M, Zhao B, et al. Multiple CRF01_AE/CRF07_BC Recombinants Enhanced the HIV-1 Epidemic Complexity Among MSM in Shenyang City, Northeast China. Front Microbiol. 12 de mayo de 2022;13:855049.

6. Qi J, Zhang D, Fu X, Li C, Meng S, Dai M, et al. High Risks of HIV Transmission for Men Who Have Sex with Men — A Comparison of Risk Factors of HIV Infection among MSM Associated with Recruitment Channels in 15 Cities of China. PLoS ONE. 2 de abril de 2015;10(4):e0121267.

7. Bowring AL, Veronese V, Doyle JS, Stoove M, Hellard M. HIV and Sexual Risk Among Men Who Have Sex With Men and Women in Asia: A Systematic Review and Meta-Analysis. AIDS Behav. 1 de octubre de 2016;20(10):2243-65.

8. Melendez-Torres GJ, Nye E, Bonell C. Is Location of Sex Associated with Sexual Risk Behaviour in Men Who Have Sex with Men? Systematic Review of Within-Subjects Studies. AIDS Behav. 1 de junio de 2016;20(6):1219-27.

9. Friedman MR, Wei C, Klem ML, Silvestre AJ, Markovic N, Stall R. HIV Infection and Sexual Risk among Men Who Have Sex with Men and Women (MSMW): A Systematic Review and Meta-Analysis. PLoS ONE. 30 de enero de 2014;9(1):e87139.

10. Ellen JM, Greenberg L, Willard N, Stines S, Korelitz J, Boyer CB, et al. Cross-sectional survey comparing HIV risk behaviours of adolescent and young adult men who have sex with men only and men who have sex with men and women in the U.S. and Puerto Rico. Sex Transm Infect. septiembre de 2015;91(6):458-61.

11. Feijoo-Cid M, Fernández-Cano MI, Zalazar V, Moriña-Soler D, García-Sierra R, Arreciado Marañón A, et al. Assessing the Underestimation of HIV Risk Infection among Young Men Who Have Sex with Men in Argentina. Int J Environ Res Public Health. 18 de noviembre de 2022;19(22):15269.

12. Mahmud S, Mohsin M, Muyeed A, Islam MM, Hossain S, Islam A. Prevalence of HIV and syphilis and their co-infection among men having sex with men in Asia: A systematic review and meta-analysis. Heliyon. 21 de febrero de 2023;9(3):e13947.

13. Mustanski BS, Newcomb ME, Bois SND, Garcia SC, Grov C. HIV in Young Men Who Have Sex with Men: A Review of Epidemiology, Risk, and Protector Factors, and Interventions. J Sex Res. marzo de 2011;48(2-3):218-53.

14. ONUSIDA. Ecuador. HIV and AIDS Estimates [Internet]. 2021 [citado 11 de abril de 2023]. Disponible en: https://www.unaids.org/es/regionscountries/countries/ecuador

15. Sanchez Gómez A. Epidemiología del VIH y sífilis en grupos más expuestos y vulnerables en Ecuador [Internet] [http://purl.org/dc/dcmitype/Text]. Universidad Rey Juan Carlos; 2014 [citado 11 de abril de 2023]. Disponible en: https://dialnet.unirioja.es/servlet/tesis?codigo=103358

16. Gutiérrez JP, Atienzo EE, Bertozzi SM, McPherson S. Effects of the Frontiers Prevention Project in Ecuador on sexual behaviours and sexually transmitted infections amongst men who have sex with men and female sex workers: challenges on evaluating complex interventions. J Dev Eff. 1 de junio de 2013;5(2):158-77.

17. Gutiérrez JP, Molina-Yepez D, Morrison K, Samuels F, Bertozzi SM. Correlates of condom use in a sample of MSM in Ecuador. BMC Public Health. 12 de junio de 2006;6(1):152.

18. Ministerio de Salud Pública-MSP. VIH – Ministerio de Salud Pública [Internet]. 2018 [citado 11 de abril de 2023]. Disponible en: https://www.salud.gob.ec/vih/

19. Hernandez I, Reina-Ortiz M, Johnson A, Rosas C, Sharma V, Teran S, et al. Risk Factors Associated With HIV Among Men Who Have Sex With Men (MSM) in Ecuador. Am J Mens Health. septiembre de 2017;11(5):1331-41.

20. Jacobson JO, Sánchez-Gómez A, Montoya O, Soria E, Tarupi W, Chiriboga Urquizo M, et al. A Continuing HIV Epidemic and Differential Patterns of HIV-STI Risk among MSM in Quito, Ecuador: An Urgent Need to Scale Up HIV Testing and Prevention. AIDS Behav. enero de 2014;18(1):88-98.

21. Montano SM, Sanchez JL, Laguna-Torres A, Cuchi P, Avila MM, Weissenbacher M, et al. Prevalences, Genotypes, and Risk Factors for HIV Transmission in South America. JAIDS J Acquir Immune Defic Syndr. 1 de septiembre de 2005;40(1):57.

22. Sánchez-Gómez A, Jacobson JO, Montoya O, Magallanes D, Bajaña W, Aviles O, et al. HIV, STI and Behavioral Risk Among Men Who have Sex with Men in a Setting of Elevated HIV Prevalence Along Ecuador’s Pacific Coast. AIDS Behav. septiembre de 2015;19(9):1609-18.

23. Feng T, Qiu Z, Meng X, Rong L. Analysis of a stochastic HIV-1 infection model with degenerate diffusion. Appl Math Comput. 1 de mayo de 2019;348:437-55.

24. Lu M, Wang Y, Jiang D. Stationary distribution and probability density function analysis of a stochastic HIV model with cell-to-cell infection. Appl Math Comput. 1 de diciembre de 2021;410:126483.

25. Wang Y, Qi K, Jiang D. An HIV latent infection model with cell-to-cell transmission and stochastic perturbation. Chaos Solitons Fractals. 1 de octubre de 2021;151:111215.

26. Dubey P, Dubey US, Dubey B. Modeling the role of acquired immune response and antiretroviral therapy in the dynamics of HIV infection. Math Comput Simul. 1 de febrero de 2018;144:120-37.

27. Deng Q, Guo T, Qiu Z, Chen Y. Towards a new combination therapy with vectored immunoprophylaxis for HIV: Modeling “shock and kill” strategy. Math Biosci. 1 de enero de 2023;355:108954.

28. Naik PA, Zu J, Owolabi KM. Modeling the mechanics of viral kinetics under immune control during primary infection of HIV-1 with treatment in fractional order. Phys Stat Mech Its Appl. 1 de mayo de 2020;545:123816.

29. Naik PA, Zu J, Ghoreishi M. Estimating the approximate analytical solution of HIV viral dynamic model by using homotopy analysis method. Chaos Solitons Fractals. 1 de febrero de 2020;131:109500.

30. Bairagi N, Adak D. Global analysis of HIV-1 dynamics with Hill type infection rate and intracellular delay. Appl Math Model. 1 de noviembre de 2014;38(21):5047-66.

31. Adak D, Bairagi N. Analysis and computation of multi-pathways and multi-delays HIV-1 infection model. Appl Math Model. 1 de febrero de 2018;54:517-36.

32. Bai N, Xu R. Backward bifurcation and stability analysis in a within-host HIV model with both virus-to-cell infection and cell-to-cell transmission, and anti-retroviral therapy. Math Comput Simul. 1 de octubre de 2022;200:162-85.

33. Alqudah MA, Aljahdaly NH. Global stability and numerical simulation of a mathematical model of stem cells therapy of HIV-1 infection. J Comput Sci. 1 de septiembre de 2020;45:101176.

34. Li MY, Wang L. Backward bifurcation in a mathematical model for HIV infection in vivo with anti-retroviral treatment. Nonlinear Anal Real World Appl. 1 de junio de 2014;17:147-60.

35. Ngina P, Mbogo RW, Luboobi LS. HIV drug resistance: Insights from mathematical modelling. Appl Math Model. 1 de noviembre de 2019;75:141-61.

36. Gomez GB, Borquez A, Caceres CF, Segura ER, Grant RM, Garnett GP, et al. The Potential Impact of Pre-Exposure Prophylaxis for HIV Prevention among Men Who Have Sex with Men and Transwomen in Lima, Peru: A Mathematical Modelling Study. Salomon JA, editor. PLoS Med. 9 de octubre de 2012;9(10):e1001323.

37. Elorreaga OA, Torres TS, Vega-Ramirez EH, Konda KA, Hoagland B, Benedetti M, et al. Awareness, willingness and barriers to HIV Self-testing (HIVST) among Men who Have Sex with Men (MSM) in Brazil, Mexico, and Peru: A web-based cross-sectional study. PLOS Glob Public Health. 2022;2(7):e0000678.

38. García MC, Duong QL, Mercer LE, Meyer SB, Ward PR. «Never testing for HIV» among men who have sex with men in Viet Nam: results from an Internet-based cross-sectional survey. BMC Public Health. 28 de diciembre de 2013;13:1236.

39. Nichols BE, Götz HM, van Gorp ECM, Verbon A, Rokx C, Boucher CAB, et al. Partner Notification for Reduction of HIV-1 Transmission and Related Costs among Men Who Have Sex with Men: A Mathematical Modeling Study. PLoS ONE. 10 de noviembre de 2015;10(11):e0142576.

40. Perry NS, Wade Taylor S, Elsesser S, Safren SA, O’Cleirigh C. The Predominant Relationship Between Sexual Environment Characteristics and HIV-Serodiscordant Condomless Anal Sex Among HIV-Positive Men Who Have Sex with Men (MSM). AIDS Behav. junio de 2016;20(6):1228-35.

41. Nguyen LH, Nguyen HLT, Larsson M, Tran BX, L Stein M, Rocha LEC, et al. An exploratory assessment of the preference for eHealth interventions to prevent HIV and sexually transmitted infections among men who have sex with men in Hanoi, Vietnam. BMC Public Health. 11 de septiembre de 2020;20(1):1387.

42. Popping S, Versteegh L, Nichols BE, van de Vijver DAMC, van Sighem A, Reiss P, et al. Characteristics and short- and long-term direct medical costs among adults with timely and delayed presentation for HIV care in the Netherlands. PloS One. 2023;18(2):e0280877.

43. Oldenburg CE, Biello KB, Perez-Brumer AG, Rosenberger J, Novak DS, Mayer KH, et al. HIV testing practices and the potential role of HIV self-testing among men who have sex with men in Mexico. Int J STD AIDS. marzo de 2017;28(3):242-9.

44. Salazar-Vizcaya L, Kusejko K, Schmidt AJ, Carrillo-Montoya G, Nicca D, Wandeler G, et al. Clusters of Sexual Behavior in Human Immunodeficiency Virus-positive Men Who Have Sex With Men Reveal Highly Dissimilar Time Trends. Clin Infect Dis Off Publ Infect Dis Soc Am. 16 de enero de 2020;70(3):416-24.

45. Holt M, Lea T, Mao L, Kolstee J, Zablotska I, Duck T, et al. Community-level changes in condom use and uptake of HIV pre-exposure prophylaxis by gay and bisexual men in Melbourne and Sydney, Australia: results of repeated behavioural surveillance in 2013–17. Lancet HIV. 1 de agosto de 2018;5(8):e448-56.

46. Luz PM, Veloso VG, Grinsztejn B. The HIV epidemic in Latin America: accomplishments and challenges on treatment and prevention. Curr Opin HIV AIDS. septiembre de 2019;14(5):366-73.

47. Bórquez A, Guanira JV, Revill P, Caballero P, Silva-Santisteban A, Kelly S, et al. The impact and cost-effectiveness of combined HIV prevention scenarios among transgender women sex-workers in Lima, Peru: a mathematical modelling study. Lancet Public Health. marzo de 2019;4(3):e127-36.

48. Carnegie NB, Goodreau SM, Liu A, Vittinghoff E, Sanchez J, Lama JR, et al. Targeting pre-exposure prophylaxis among men who have sex with men in the United States and Peru: partnership types, contact rates, and sexual role. J Acquir Immune Defic Syndr 1999. 1 de mayo de 2015;69(1):119-25.

49. Luz PM, Osher B, Grinsztejn B, Maclean RL, Losina E, Stern ME, et al. The cost‐effectiveness of HIV pre‐exposure prophylaxis in men who have sex with men and transgender women at high risk of HIV infection in Brazil. J Int AIDS Soc. 30 de marzo de 2018;21(3):e25096.

50. Feng Z, Xu D, Zhao H. Epidemiological models with non-exponentially distributed disease stages and applications to disease control. Bull Math Biol. julio de 2007;69(5):1511-36.

51. Selinger C, Katze MG. Mathematical models of viral latency. Curr Opin Virol. 1 de agosto de 2013;3(4):402-7.

52. Tan WY, Wu H. Deterministic and Stochastic Models of AIDS Epidemics and HIV Infections with Intervention [Internet]. Deterministic and stochastic models of AIDS epidemics and HIV infections with intervention. Singapore: World Scientific; 2005 [citado 11 de abril de 2023]. 612 p. Disponible en: https://www.worldscientific.com/doi/epdf/10.1142/5737

53. WHO. HIV, Estimated antiretroviral therapy coverage among people living with HIV (%) [Internet]. 2016 [citado 11 de abril de 2023]. Disponible en: https://www.who.int/data/gho/data/indicators/indicator-details/GHO/estimated-antiretroviral-therapy-coverage-among-people-living-with-hiv-(-)

54. Yaghoobi H, Ahmadinia H, shabani Z, Vazirinejad R, Safari R, Shahizadeh R, et al. Life expectancy and years of life lost in HIV patients under the care of BandarAbbas Behavioral Disorders Counseling Center. Nepal J Epidemiol. 31 de diciembre de 2017;7(4):702-12.

55. Mohammadi-Moein HR, Maracy MR, Tayeri K. Life expectancy after HIV diagnosis based on data from the counseling center for behavioral diseases. J Res Med Sci Off J Isfahan Univ Med Sci. diciembre de 2013;18(12):1040-5.

56. Smiley CL, Rebeiro PF, Cesar C, Belaunzaran-Zamudio PF, Crabtree-Ramirez B, Padgett D, et al. Estimated life expectancy gains with antiretroviral therapy among adults with HIV in Latin America and the Caribbean: a multisite retrospective cohort study. Lancet HIV. 1 de mayo de 2021;8(5):e266-73.

57. Blower SM, Dowlatabadi H. Sensitivity and Uncertainty Analysis of Complex Models of Disease Transmission: An HIV Model, as an Example. Int Stat Rev Rev Int Stat. 1994;62(2):229-43.

58. Instituto Nacional de Estadística y Censos I. Compendio Estadístico 2014 [Internet]. Instituto Nacional de Estadística y Censos. 2014 [citado 11 de abril de 2023]. Disponible en: https://www.ecuadorencifras.gob.ec/compendio-estadistico-2014/

59. Coriat B. The Political Economy of HIV/AIDS in Developing Countries [Internet]. Edward Elgar Publishing; 2008 [citado 11 de abril de 2023]. 352 p. Disponible en: https://www.e-elgar.com/shop/gbp/the-political-economy-of-hiv-aids-in-developing-countries-9781848440777.html

60. Chibawara T, Mbuagbaw L, Kitenge M, Nyasulu P. Effects of antiretroviral therapy in HIV-positive adults on new HIV infections among young women: a systematic review protocol. Syst Rev. 5 de marzo de 2019;8(1):68.

61. Tefera E, Mavhandu-Mudzusi AH. Experiences of Antiretroviral Therapy Initiation Among HIV-Positive Adults in Ethiopia: A Descriptive Phenomenological Design. HIVAIDS - Res Palliat Care. 24 de mayo de 2022;14:243-54.

62. Blower S. Calculating the consequences: HAART and risky sex. AIDS. 6 de julio de 2001;15(10):1309.

63. Sanders GD, Bayoumi AM, Sundaram V, Bilir SP, Neukermans CP, Rydzak CE, et al. Cost-Effectiveness of Screening for HIV in the Era of Highly Active Antiretroviral Therapy. N Engl J Med. 10 de febrero de 2005;352(6):570-85.

64. Matasariu DR, Onofriescu M, Mihalceanu E, Schaas CM, Bujor IE, Tibeica AM, et al. Impact of HAART Therapy and HIV Infection over Fetal Growth—An Anthropometric Point of View. Microorganisms. junio de 2022;10(6):1123.

65. Bobashev G. Simulation Modeling of HIV Infection—From Individuals to Risk Groups and Entire Populations. En: Quantitative Methods for HIV/AIDS Research. Chapman and Hall/CRC; 2017.

66. Biello KB, Oldenburg CE, Mitty JA, Closson EF, Mayer KH, Safren SA, et al. The “Safe Sex” Conundrum: Anticipated Stigma From Sexual Partners as a Barrier to PrEP Use Among Substance Using MSM Engaging in Transactional Sex. AIDS Behav. enero de 2017;21(1):300-6.

67. Edeza A, Karina Santamaria E, Valente PK, Gomez A, Ogunbajo A, Biello K. Experienced barriers to adherence to pre-exposure prophylaxis for HIV prevention among MSM: a systematic review and meta-ethnography of qualitative studies. AIDS Care. 3 de junio de 2021;33(6):697-705.

68. Babel RA, Wang P, Alessi EJ, Raymond HF, Wei C. Stigma, HIV Risk, and Access to HIV Prevention and Treatment Services Among Men Who have Sex with Men (MSM) in the United States: A Scoping Review. AIDS Behav. 2021;25(11):3574-604.

Received: 25 June 2023/ Accepted: 26 August 2023 / Published:15 September 2023

Citation: Morey-León, G.; Vega-Lugo, J.; Humberstone, J.; Gonzalez-Gonzalez,M.; Morales-Butler, E.; Paredes, M.; Mubayi, A.; Seshaiyer, P. Modelamiento matemático del efecto del retraso del tratamiento sobre la resistencia del VIH a drogas en hombres que tienen sexo con hombres ecuatorianos. Revis Bionatura 2023;8 (3) 103 http://dx.doi.org/10.21931/RB/2023.08.03.103